İstifadə ediləcək bəzi terminlərin qarşılığı:
- binary tree – ikili ağac
- Binary Search Tree (BST) – ikili axtarış ağacı
- root – kök
- node – düyün
- left-child – sol budaq
- right-child – sağ budaq
- walk, traverse – gəzişmə
Binary Search Tree (BST) mövzusunu oxuyarkən ağac üzərində gəzişməklə (ingiliscə “walk” və ya “traverse” adlanır) bağlı hissə diqqətimi çəkdi, fikirləşdim rekursiya ilə bağlı örnək verilməsi baxımından gözəl nümunə ola bilər. Blogda rekursiv metodlarla bağlı bir yazı paylaşmışdım, BST mövzusunda rast gəldiyim rekursiv metodlar isə daha irəli səviyyə rekursiyaya uyğun nümunələr idi. Ona görə də bu mövzu barədə bir az araşdırma edib həmin mövzunun davamı olaraq yazmaq qərarına gəldim. Bu yazımızdakı rekursiv nümunələr BST ilə əlaqəli olduğundan ilk növbədə qısa şəkildə BST mövzusuna nəzər salacağıq.
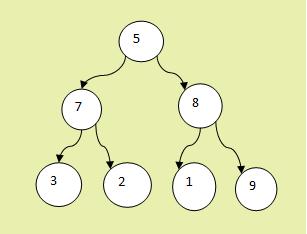
İkili axtarış ağacı (BST) ikili ağacın (binary tree) xüsusi bir halıdır. İkili ağac iyerarxik struktura malikdir və şəkildən də göründüyü kimi bu strukturda hər düyün (node) maksimum iki budaqdan (left-child, right-child) ibarət ola bilər, iyerarxiyanın başındakı 1-ci düyün (the topmost node) isə kök (root) adlanır:
Şəkil 1. İkili ağac (binary tree) 1
Yuxarıdakı şəkildə ‘5’ düyün (node), ‘7’ (left-child) və ‘8’ (right-child) isə onun budaqları hesab olunur. Eyni zamanda ‘7’ ‘5’-ə nəzərə budaq hesab edilsə də ‘3’ və ‘2’-yə nəzərən düyündür. Həmçinin də ‘8’, ‘1’ və ‘9’ ‘8’-in budaqlarıdır.
Bəs ikili axtarış ağacı (BST) nədir?
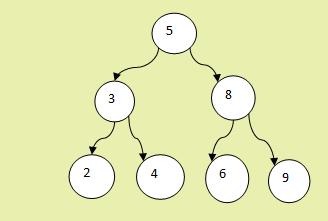
Yuxarıdakı şəkildən görünür ki, rəqəmlərin düzülüşündə hər hansı xüsusi bir qayda mövcud deyil. İkili axtarış ağacının ikili ağacdan fərqi ondadır ki, rəqəmlər xüsusi qanunauyğunluğa görə düzülməlidir:
kökdəki dəyər sol budaqdakı dəyərdən böyük (bərabər), sağ budaqdakı dəyərdən kiçik (bərabər) olmalıdır (burada bərabər olma şərtinin özü belə müzakirə mövzusudur, bəzi mənbələrdə dəyərlərin unikal olması fikri irəli sürülür, amma mən “Introduction to Algorithms” kitabına istinadən yazmışam2).
Şəkil 2. İkili axtarış ağacı (Binary Search Tree) 3
Gördüyünüz kimi qeyd etdiyimiz şərtlər ödənilir:
- 3 (left) < 5 (node) < 8 (right)
- 2 (left) < 3 (node) < 4 (right)
- 6 (left) < 8 (node) < 9 (right)
Həmçinin 5-dən soldakı bütün dəyərlər 5-dən kiçik olmalıdır. Misal üçün 4 əvəzinə 7 ola bilməz. Məhz bu struktur sayəsində BST-də axtarış əməliyyatlarını O(h) (h – ağacın hündürlüyüdür) zamanda həyata keçirmək mümkündür. Balanslaşdırılmış ikili axtarış ağaclarında isə bu zaman O(lgn)-dir.
BST üzərində aparılan əsas əməliyyatlar axtarış (Search), ən kiçik elementin tapılması (Minimum), ən böyük elementin tapılması (Maximum), qeyd edilən elementdən sonrakı ən kiçik (Successor) və yaxud əvvəlki ən böyük (Predecessor) elementin tapılması, yeni elementin əlavə edilməsi (Insert), mövcud elementlərdən hər hansı birinin silinməsi (Delete) və s-dir. Bunlarla bağlı internetdə kifayət qədər zəngin məlumatlar var. Bir balaca haşiyəyə çıxaraq qeyd edim ki, buna görə ən böyük minnətdarlıqlardan biri Youtube`nin payına düşür. Bildiyiniz kimi Youtube kanalında reklamların paylaşımına icazə verməklə qazanc əldə etmək mümkündür. Və məhz Youtube-un bu siyasəti sayəsində bir-biri ilə rəqabətə girən kanalların sayı get-gedə artır və daha çox izləyici cəlb etmək məqsədilə kanallar daha fərqli metodlar tətbiq etməyə, daha effektiv ola biləcək üsullarla izah etməyə çalışırlar. Və son nəticədə də keyfiyyətli “tutorial”lar meydana çıxır və bundan da ən çox qazanan izləyicilər olur. Bu mövzulara həmin kanallardan detallı baxa bilərsiniz. Bizim mövzumuz rekursiya ilə bağlı olduğundan biz bu yazımızda əsasən ikili axtarış ağacının elementlərinin (keys) çap edilməsinə baxacağıq. Bunun üçün belə deyək, ağacın budaqlarında gəzişməli olacağıq. İngiliscə buna “walk” və yaxud “traverse” deyilir.
Gəzişmələrin bir neçə növü mövcuddur. Bu gəzişmə növlərinə və rekursiyanın köməkliyi ilə hər gəzişmə növü üzrə elementlərin çap edilməsinə aşağıda bir-bir ətraflı baxacağıq. Amma əvvəlcə bir məqamı qeyd etmək istəyirəm. BST ilə əlaqəli oxuduğum, baxdığım və araşdırdığım bütün mənbələrdə BST nümunələrinin hamısı “linked list” (türkcə “bağlı liste”) istifadə edilərək yazılmışdı, çünki linked list BST-ni saxlamaq üçün optimal “data structures” hesab edilir. Amma mən kodumuzun daha qısa və rekursiyanın daha anlaşıqlı olması üçün massivlərdən istifadə etməyi qərara almışam. BST strukturu üçün adətən massivlərin istifadə edilməsi optimallıq baxımından əlverişli hesab edilmir, çünki yeni düyünün əlavə edilməsi yaxud mövcud düyünün silinməsi linked list`ə nəzərən xeyli “məsrəflidir”. Amma biz nümunəmizdə BST-ni ancaq elementlərin çap edilməsi üçün istifadə edəcəyimizdən elə də bir qorxusu yoxdur
Heapsort mövzusunu oxuyarkən binary heap strukturunu görmüşdüm və həmin mövzuda binary heap strukturunun həm ikili ağac (binary tree), həm də massiv (array) üzərində qurulmuş nümunəsi verilmişdi:
Şəkil 3. Max-heap strukturunun ikili ağac (a) və massiv (b) şəklində ifadəsi4
Bizə massiv üzərində mənimsədilmiş nümunə maraqlıdır, çünki biz aydınlaşdırmaq istəyirik ki, eyni mənimsədilmə məntiqini BST üzərində tətbiq edə bilərik ya yox. Amma əvvəlcə binary heap nədir, onu BST ilə əlaqələndirə bilərik ya yox onu özümüz üçün təyin etməliyik.
Binary heap özü də bir ikili ağacdır, amma əsas iki özəlliyi var.
Birinci özəlliyi odur ki, “complete binary tree”-dir. “Complete binary tree” üçün kitabda belə bir tərif keçir:
“The tree is completely filled on all levels except possibly the lowest, which is filled from the left up to a point”. 5
Yəni sonuncu səviyyədən (level) başqa bütün səviyyələrdə ağac dolu olmalıdır. Sonuncu səviyyədə isə ağaca budaqların əlavə edilməsinə ən soldan başlanılmalıdır. Məhz bu özəllik sayəsində “binary heap”ləri rahatlıqla massivlərdə saxlamaq mümkündür.
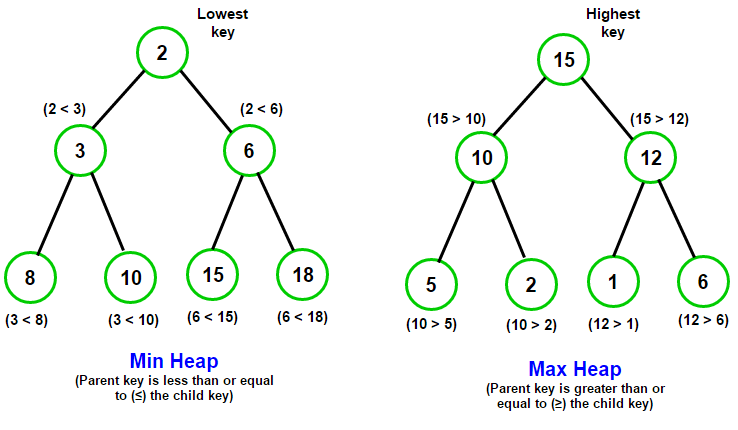
İkinci özəlliyi isə düyünlərin dəyərlərinə (keys) görə müəyyən ardıcıllıqla düzülməsindədir. Binary heap-in iki növü var: max-heap və min-heap. BST üçün qeyd etmişdik ki, kökdə duran element sol budaqdakı elementdən böyük (bərabər), sağ budaqdakı elementdən isə kiçik (bərabər) olmalıdır. Binary heap üçün bu qayda bir az fərqlidir. Max-heap strukturunda kökdə duran element istənilən halda həm sağ, həm də sol budaqdakı elementdən böyük (bərabər) olmalıdır. Min-heap strukturunda isə bunun tərsidir, kökdə duran element istənilən halda həm sağ, həm də sol budaqdakı elementdən kiçik (bərabər) olmalıdır. Şəkil 3-də qeyd olunan max-heap strukturudur. Max-heap və min-heap strukturuna müqayisəli şəkildə baxmaq üçün aşağıdakı görüntü gözəl örnəkdir:
Şəkil 4. Min-heap və Max-heap nümunəsi6
Nəticə olaraq təyin etdik ki, həm binary-heap, həm də BST hər ikisi bir ikili ağacdır və eyni mənimsədilmə məntiqini BST üçün də tətbiq etmək olar, sadəcə BST nümunəmiz “complete binary tree” olmalıdır. İndi isə qayıdaq 3-cü şəkildəki mənimsədilmə məsələsinə. Gördüyünüz kimi şəkildə ikili ağacdakı dəyərlərin massivə necə yerləşdirilməsi göstərilib: dəyərlər düyünlərin üzərində göstərilmiş rəqəmlərin ardıcıllığına uyğun massivə sıra ilə əlavə edilib, yəni düyünlərin üzərindəki rəqəmlər eyni zamanda massivdəki indeksləri bildirir. Əlavə məlumat üçün bu videoya baxa bilərsiniz (Bu youtube kanalındakı videolar səssiz hazırlansa da çox gözəl izahları olur).
İndi isə qalır ən vacib məsələlərdən biri; BST üzərində gəzişmək üçün bizə hər düyünün sol və sağ budaqlarını bilmək mütləq lazımdır. Bəs massiv üzərində bunu necə təyin edəcəyik?
Bunun çox sadə şəkildə tapılması üsulu var (k – key, i – indeksi bildirir):
node(k) = i
left = i * 2;
right = i * 2 + 1;
Əgər düyünümüz massivin i-ci indeksindədirsə, onun sol budağı (i*2), sağ budağı isə (i*2 + 1)-ci indeksdə olacaqdır7. Misal üçün şəkil 3-də 8 dəyərinə malik düyünün budaqlarını tapaq:
node(8) = 4
left = 4 * 2 = 8 --> 2
right = 4 * 2 + 1 = 9 --> 4
Bununla da BST-nin massiv üzərində mənimsədilməsi, hər düyünün sol və sağ budaqlarının necə təyin edilməsi məsələləri həll edildi. Artıq BST üzərində gəzişmələrə keçə bilərik.
Traverse Binary Search Tree
İkili axtarış ağacları elementlərinin (keys) çap edilməsi üçün 3 cür gəzişmə mövcuddur:
- Inorder (Left, Root, Right)
- Preorder (Root, Left, Right)
- Postorder (Left, Right, Root)
Oxuduğum türkcə kitablardan birində bu gəzişmələr (“dolaşmalar”) “öncə-kök”, “ortada-kök”, “sonra-kök” kimi qeyd olunub8, digərində isə “sıralı ağac yürüyüşü”, “ön sıra ağac yürüyüşü” və “son sıra ağac yürüyüşü” kimi tərcümə edilib9. Terminlərin çevrilməsində fərqliliklər, optimal əvəzetmənin tapılması problemi hələ də qalmaqdadır. Mən də qarşılıq olaraq “traverse” və ya “walk” əvəzinə “gəzişmə” sözünü istifadə edirəm, nə dərəcədə uyğundur bilmirəm
Inorder Tree Walk
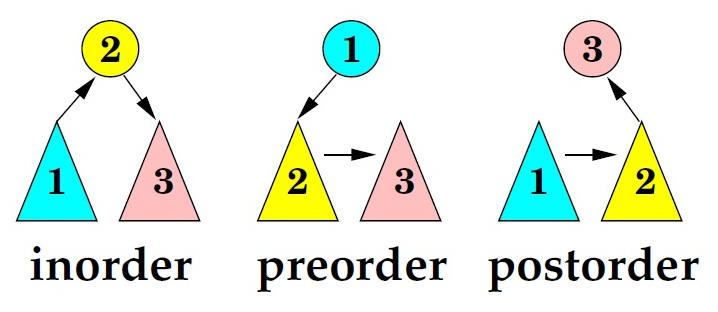
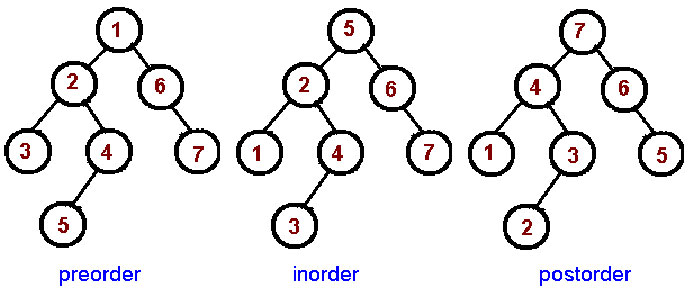
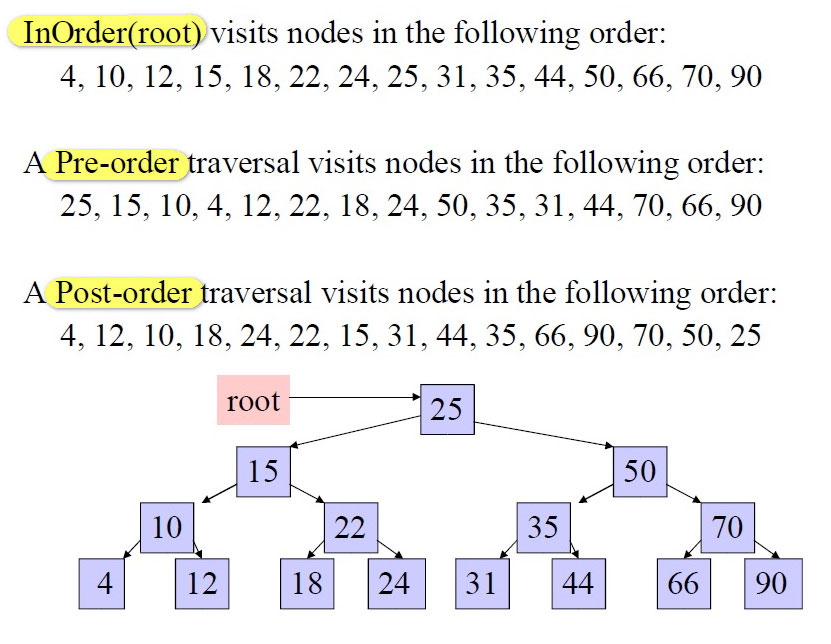
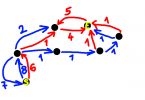
Bu gəzişmə üsulu Left –> Root –> Right ardıcıllığına uyğun olaraq elementləri çap edir. Yəni əvvəlcə sol budaqdakı element, sonra kökdə dayanan element, ən son isə sağ budaqdakı element çap edilir. Bu gəzişmə növündə elementlər sort olunmuş formada çap edilir, bu da BST-nin strukturundan irəli gəlir. Aşağıda gəzişmələrin ardıcıllığı nömrələnmiş şəkildə göstərilib:
Şəkil 5. Gəzişmələr (traverse)10
Yuxarıdakı şəkil ardıcıllığı başa düşmək üçün yaxşı nümunədir, amma BST-də düyünlərin sayı çoxaldıqca ardıcıllığı başa düşmək getdikcə çətinləşir. Amma bir az zaman ayırıb, oxuyub-araşdırdıqdan sonra rahatlıqla məntiqini tutmaq mümkündür. Deyəsən bu mövzumuz şəkillərlə bol olan yazılarımızdan biri olacaq, fikirləşirəm “şəkil” fikri izah etmək üçün “sözlər”dən daha effektiv vasitədir. Mövzunu araşdırarkən “Carnegie Mellon University” professorlarından birinin yazısında gəzişmələrlə bağlı bir şəkil gördüm, mənə kömək elədi, sizə də kömək edəcəyini güman edib onu da paylaşmaq qərarına gəldim. Rəqəmlərin ardıcıllığı düyünlərin (elementlərin) çap edilmə ardıcıllığını bildirir:
Şəkil 6. BST üzərində gəzişmələr11
Alqoritmləri oxumağa başlayandan bu yana təcrübədən görmüşəm ki, alqoritmi başa düşmək üçün ən effektiv üsullardan biri də animasiyalı görüntüdür. Ona görə də hər gəzişmə üçün internetdən optimal animasiya nümunəsi tapmışam və hər gəzişmə üçün bir-bir əlavə edəcəm. Inorder gəzişməsində elementlər aşağıdakı ardıcıllıqla çap edilir:
Preorder Tree Walk
Bu gəzişmə üsulu Root –> Left –> Right ardıcıllığına uyğun olaraq elementləri çap edir. Yəni əvvəlcə kökdə dayanan element, sonra sol budaqdakı element, ən son isə sağ budaqdakı element çap edilir. Bu da animasiyalı görüntü:
Postorder Tree Walk
Bu gəzişmə üsulu isə Left –> Right –> Root ardıcıllığına uyğun olaraq elementləri çap edir. Yəni əvvəlcə sol budaqdakı element, sonra sağ budaqdakı element, ən son isə kökdə dayanan element çap edilir. Bu animasiyanı isə çox bəyənirəm, çox gözəl hazırlanıb:
Rekursiyanın istifadə edilməsi
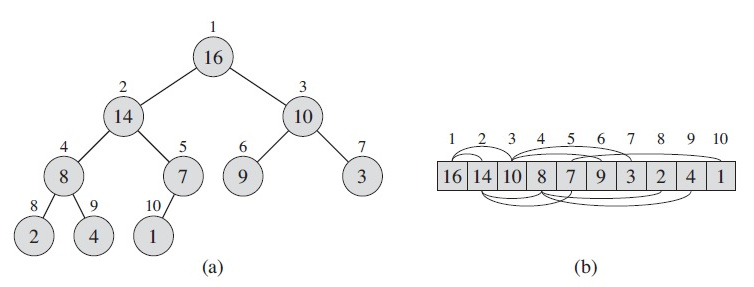
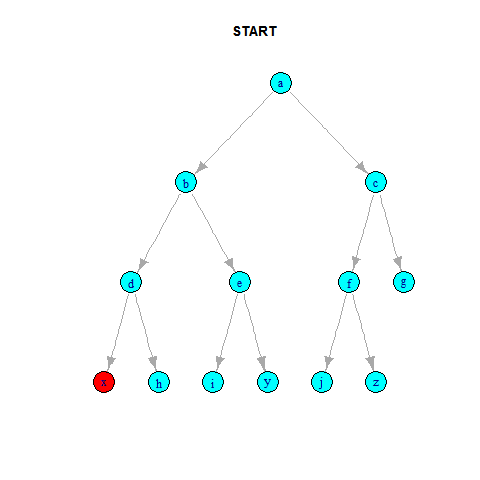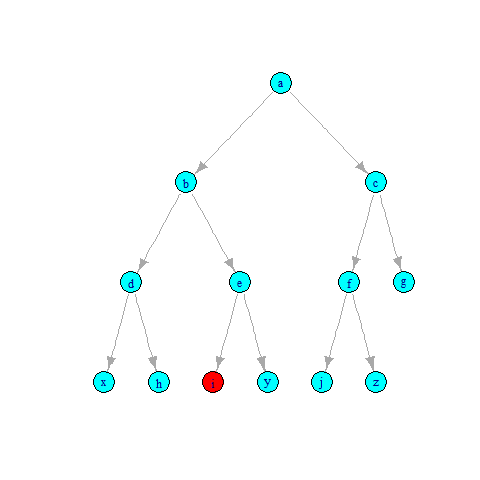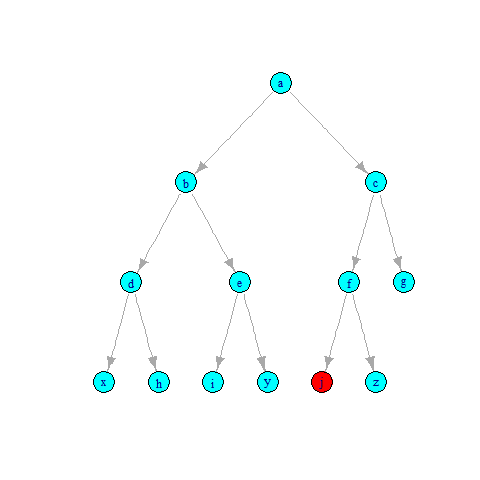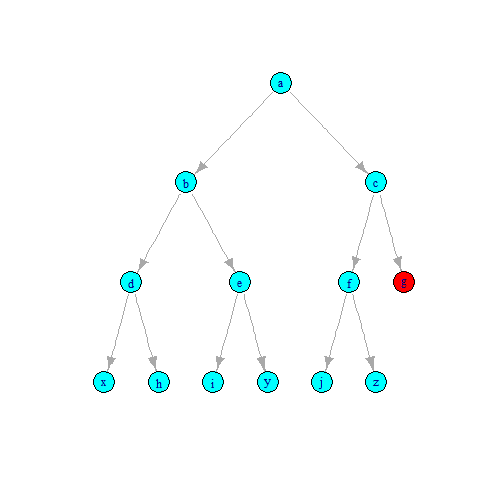
İndi isə yuxarıda qeyd etdiyimiz gəzişmələr ilə bağlı bir nümunə götürək və Java`da rekursiv metodlar vasitəsilə kodlaşdırılmasına baxaq. Aşağıdakı screenshot-u başqa bir universitet professorunun yazısından nümunə üçün götürmüşəm. Screenshot`da bir BST nümunəsi və hər 3 gəzişmə üzrə elementlərin çap olunma ardıcıllığı verilib:
Şəkil 7. BST üzərində gəzişmə nümunəsi12
Nümunəmiz “complete binary tree” olduğundan massivə mənimsədilməsində çox güman problem yaşamayacağıq. Biz indi bu BST nümunəsinin Java`da massivə mənimsədilməsinə və daha sonra hər üç gəzişmə üzrə rekursiv metodlar vasitəsilə elementlərin çap edilməsinə baxaq. Sonda isə kodumuzun output`u ilə bu screenshot`dakı nəticələri müqayisə edək və kodumuzun düzgün işləyib işləmədiyini öyrənək.
Bir məqamı öncədən qeyd edim. Bir çox proqramlaşdırma dilində indekslər sıfırdan başlayır, həmçinin Java`da. Amma “Introduction to algoritms” kitabındakı izahlarda indekslər əsasən 1-dən başlayır. 3-cü şəkildəki binary-heap nümunəsində də 1-dən başlayır, çünki belə olan halda sol və sağ budaqların tapılması daha rahat olacaq. Biz də kodun daha rahat başa düşülməsi məqsədilə ikili ağac üzərindəki dəyərlərin massivə mənimsədilməsinə 1-ci indeksdən başlayacağıq:
package az.mm.algoritms;
public class BinarySearchTree {
private static int[] bst = {0, 25, 15, 50, 10, 22, 35, 70, 4, 12, 18, 24, 31, 44, 66, 90};
/*
InOrder: 4, 10, 12, 15, 18, 22, 24, 25, 31, 35, 44, 50, 66, 70, 90
Pre-order: 25, 15, 10, 4, 12, 22, 18, 24, 50, 35, 31, 44, 70, 66, 90
Post-order: 4, 12, 10, 18, 24, 22, 15, 31, 44, 35, 66, 90, 70, 50, 25
*/
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
int root = 1; // 0 deyil, 1 olacaq, çünki root dəyərimiz 1-ci indeksdən başlayır
System.out.print("level-order:\t");
bst.levelOrderWalk(root);
System.out.print("\nin-order:\t");
bst.inOrderWalk(root);
System.out.print("\npre-order:\t");
bst.preOrderWalk(root);
System.out.print("\npost-order:\t");
bst.postOrderWalk(root);
}
public void levelOrderWalk(int i){
if(i >= bst.length) return;
print(i);
levelOrderWalk(++i);
}
public void inOrderWalk(int i){
if(i >= bst.length) return;
inOrderWalk(left(i));
print(i);
inOrderWalk(right(i));
}
public void preOrderWalk(int i){
if(i >= bst.length) return;
print(i);
preOrderWalk(left(i));
preOrderWalk(right(i));
}
public void postOrderWalk(int i){
if(i >= bst.length) return;
postOrderWalk(left(i));
postOrderWalk(right(i));
print(i);
}
private void print(int i){
System.out.print(bst[i] + " ");
}
/* 0-cı indeksdən başlamaq üçün:
* left: 2*(i+1)-1
* right: 2*(i+1)
* Bu zaman root dəyər 1 deyil, 0 olacaq
*/
private int left(int i) { return 2*i; }
private int right(int i) { return 2*i+1; }
}
Output:
level-order: 25 15 50 10 22 35 70 4 12 18 24 31 44 66 90
in-order: 4 10 12 15 18 22 24 25 31 35 44 50 66 70 90
pre-order: 25 15 10 4 12 22 18 24 50 35 31 44 70 66 90
post-order: 4 12 10 18 24 22 15 31 44 35 66 90 70 50 25
Kodumuzun output`unu şəkil 7-dəki nəticə ilə yoxlasaq görərik ki, nəticəmiz doğrudur. Rekursiv metodların köməkliyi ilə çox az kod yazmaqla və çox xırda dəyişikliklər etməklə BST-nin elementlərini 3 (level-order`i nəzərə almasaq) fərqli şəkildə çap etdik. Rekursiya istifadə etmədən də elementləri çap etməyin üsulları mövcuddur. Bu üsullar üçün belə “data structures” olaraq Stack istifadə olunur, çünki bu problemin həlli üçün optimal strukturdur. Amma biz rekursiv metodlardan istifadə etdikdə stack ilə bağlı işləri bizim əvəzimizə kompilyator özü görür. Nə rekursiya, nə də Stack istifadən etmədən də həll üsulları mövcuddur. Bunlardan biri “Morris Traversal” adlanır və bu üsulda “Threaded Binary Tree” istifadə edilir. Ətraflı bu linkdən baxa bilərsiniz.
İndi isə qayıdaq əsas məsələ – rekursiyanın necə işləməsinin izahına. Daha yaxşı olar ki, rekursiya istifadə etmədən Stack ilə olan bir kod nümunəsinə baxaq və Stack-in rolunun nədən ibarət olduğunu görək. Ümid edirəm bu bizə rekursiya zamanı stack-in necə işləməsini daha yaxşı başa düşməyə kömək edəcək. Nümunə üçün yuxarıdakı 1-ci – inOrderWalk(int ) metodumuzu götürək. Həmin metodu rekursiya istifadə etmədən aşağıdakı şəkildə yaza bilərik:
public void inOrderWalkWithoutRecursion(int i) {
Stack<Integer> stack = new Stack<Integer>();
while (!stack.isEmpty() || i < bst.length)
if (i < bst.length) {
stack.push(i);
i = 2*i; //left
} else {
i = stack.pop();
System.out.print(bst[i] + " ");
i = 2*i+1; //right
}
}
Gördüyünüz kimi bu metodda Stack yaradırıq və müəyyən şərtlər yoxlanıldıqdan sonra dəyərlər Stack`ə əlavə edilir (push) və çıxarılır (pop). Amma dəyərlərin Stack əlavə edilib çıxarılmasında hər hansı bir ardıcıllıq yoxdur, sırf şərtlərdən asılı olaraq dəyişir. Əvvəlki mövzumuzda da qeyd etmişdik ki, pop() metodu çağırıldıqda ən son əlavə edilən dəyəri Stack`dən çıxarır. Yəni bütün bunları “manual” olaraq biz özümüz edirik. Amma rekursiv metodlardan istifadə etdikdə yuxarıda da qeyd etdiyimiz kimi bütün bunların hamısını kompilyator bizim əvəzimizə edir. Bəs bütün bunlar necə baş verir?
Əvvəla qeyd edim ki, bu nümunəmizdəki rekursiv metodlar əvvəlki mövzudakı nümunələrə nisbətən daha qarışıqdır, çünki həm sol, həm də sağ budaq üçün rekursiv metodlar ayrı-ayrılıqda çağırılır, yəni iki dəfə:
public void inOrderWalk(int i){
if(i >= bst.length) return;
inOrderWalk(left(i));
print(i);
inOrderWalk(right(i));
}
Buna “multiple recursion” da deyilir, əvvəlki mövzuda baxdıqlarımız isə “single recursion“a aid nümünələr idi. Bəs bunlar arasında performans baxımından bir fərq varmı sualı sizi maraqlandırırsa, Wikipedia`da belə bir maraqlı fakta rast gəldim:
Single recursion is often much more efficient than multiple recursion, and can generally be replaced by an iterative computation, running in linear time and requiring constant space. Multiple recursion, by contrast, may require exponential time and space, and is more fundamentally recursive, not being able to be replaced by iteration without an explicit stack. 13
Necə işləməsinə gəldikdə isə sol budaq üçün rekursiya işə düşür və if şərti ödənilənə qədər davam edir. if şərti true olduqda rekursiya bitir və print ifadəsi icra edilir. Ardınca isə sağ budaq üçün rekursiya başlayır. Burada iki hal baş verir:
ifşərtitrueqaytararsa rekursiya bitir;- əks halda yenidən sol budaq üçün rekursiya işə düşür.
Metod iç-içə şəkildə özü-özünü təkrar-təkrar çağırdığından push() və pop() metodları hər hansı bir ardıcıllıq izləmədən işləyir, yəni bir neçə dəyər əlavə edilir, sonra biri çıxarılır, sonra təzədən əlavə edilir və s. Ardıcıllığın hansı şəkildə baş verdiyini izah etmək üçün yenə ənənəvi üsulumdan istifadə edəcəm; metoda print ifadələri əlavə edib izaha onun üzərindən davam edəcəyik. Nümunə üçün kodda istifadə etdiyimiz ikili ağacı götürək. Amma output`umuzun böyük olmaması üçün ağacın sonuncu “level”ini (hündürlük yaxud dərinlik) çıxaraq, yəni 70 sonuncu elementimiz olsun:
package az.mm.algoritms.treetraversals;
public class BSTraversalExplain {
private static int[] bst = {0, 25, 15, 50, 10, 22, 35, 70};
public static void main(String[] args) {
BSTraversalExplain bst = new BSTraversalExplain();
int root = 1;
bst.inOrderWalk(root);
}
public void inOrderWalk(int i){
if(i >= bst.length) return;
inOrderWalk(left(i));
print(i);
inOrderWalk(right(i));
}
private void print(int i){
System.out.printf("%d is popped from stack and print \n", bst[i]);
}
private int left(int i) {
if(2*i < bst.length)
System.out.printf("left-child(%d) is pushed to stack \n", bst[2*i]);
else
System.out.printf("left-child of '%d' not exists! \n", bst[i]);
return 2*i;
}
private int right(int i) {
if(2*i+1 < bst.length)
System.out.printf("right-child(%d) is pushed to stack \n", bst[2*i+1]);
else
System.out.printf("right-child of '%d' not exists! \n", bst[i]);
return 2*i+1;
}
}
Output:
left-child(15) is pushed to stack
left-child(10) is pushed to stack
left-child of '10' not exists!
10 is popped from stack and print
right-child of '10' not exists!
15 is popped from stack and print
right-child(22) is pushed to stack
left-child of '22' not exists!
22 is popped from stack and print
right-child of '22' not exists!
25 is popped from stack and print
right-child(50) is pushed to stack
left-child(35) is pushed to stack
left-child of '35' not exists!
35 is popped from stack and print
right-child of '35' not exists!
50 is popped from stack and print
right-child(70) is pushed to stack
left-child of '70' not exists!
70 is popped from stack and print
right-child of '70' not exists!
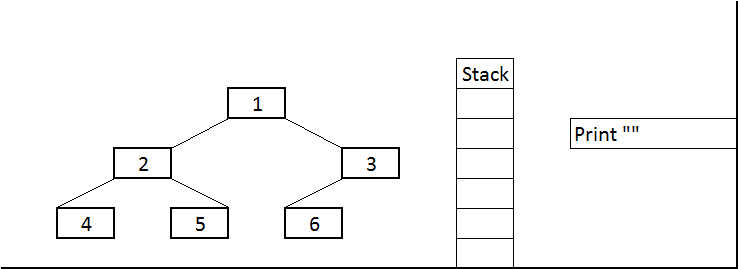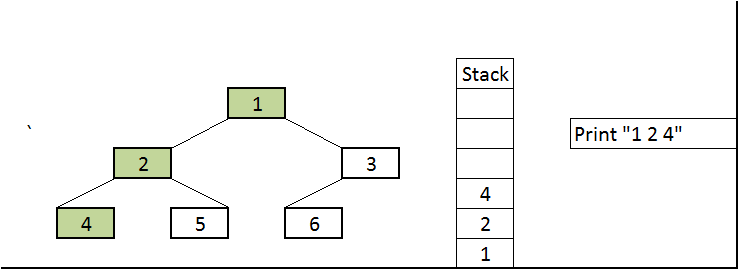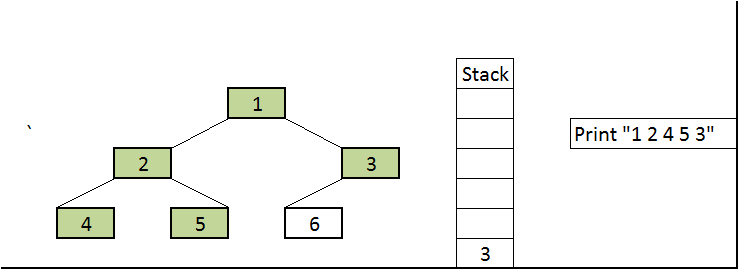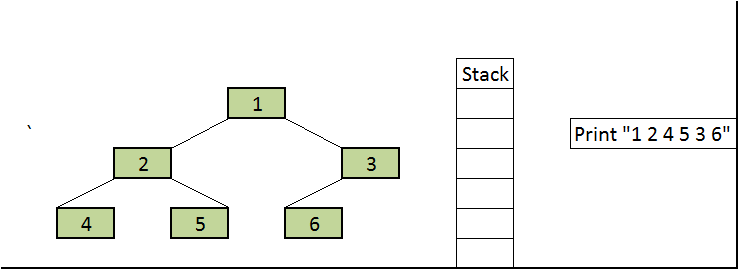
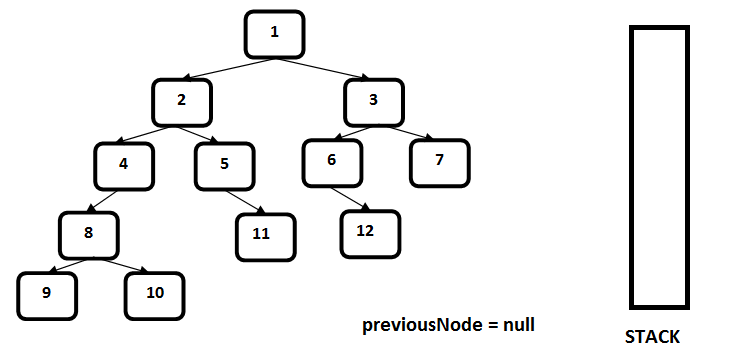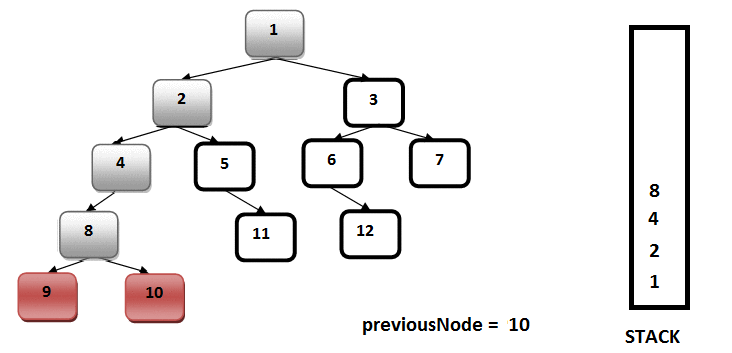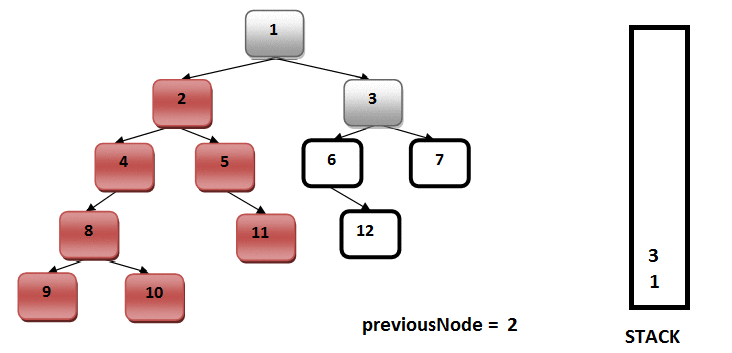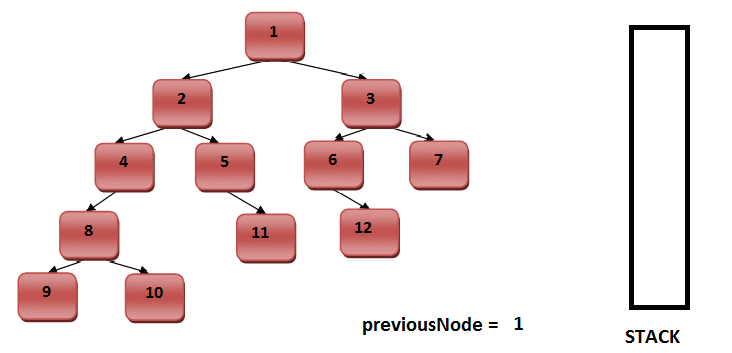
Root dəyərimiz (25) inOrderWalk(int ) metodu birinci dəfə main metoddan çağırılanda stack yaddaşa əlavə edilir, ona görə də output-da onun “push” edildiyi görsənmir. İşləmə ardıcıllığına gəldikdə isə birinci sol budaq üçün rekursiya işə düşür və root elementimiz 25-in sol budağının olub olmaması yoxlanılır. 25-in sol budağı var və 15-dir, 15 stack yaddaşa əlavə edilir (əslində biz kodda stack yaddaşa dəyərləri deyil, indeksləri əlavə etmişik, amma anlaşıqlı olması üçün dəyərlər üzərindən izah edilir). Sonra 15-in sol budağı yoxlanılır və 10 stack yaddaşa əlavə edilir. Daha sonra 10-un sol budağının olub olmaması yoxlanılır. 10-nun sol budağı yoxdur və if şərtinə daxil olur və rekursiya bitir. Ardınca print ifadəsi çağırılır. Stack yaddaşa ən son əlavə edilən 10 idi və 10 stack yaddaşdan çıxarılır və print edilir. Print ifadədən sonra sağ budaq üçün rekursiya başlanır və 10-nun sağ budağının olub olmaması yoxlanılır. 10-nun sağ budağı yoxdur və rekursiya bitir.
Həm sol, həm də sağ budaq üçün rekursiya bitsə də bizim stack yaddaşda hələ elementlərimiz qalıb. Ümumiyyətlə, stack yaddaşdan bütün elementlər çıxarılanadək print ifadəsi çağırılacaq. 10 elementi stack`dən çıxarıldıqdan sonra stack`dəki ən son element 15 olmuşdu. Ona görə də pop() metodu çağırıldıqda 15 çıxarılır və print edilir. Daha sonra 15-in sağ budağının olub olmamasının yoxlanılması üçün rekursiya işə düşür. Və proses bu minvalla ağacdakı bütün elementlər qurtaranadək davam edir.
Bu mövzunun da beləcə sonuna çatdıq. Ümid edirəm faydalı olacaqdır. Uğurlar!
Github link:
https://github.com/mmushfiq/BSTraversal
1http://bilgisayarkavramlari.sadievrenseker.com/2008/05/07/ikili-agac-binary-tree/
2 “Introduction to Algorithms” (MIT Press), 3-cü nəşr, səhifə 287
3 http://bilgisayarkavramlari.sadievrenseker.com/2008/05/07/ikili-arama-agaci-binary-search-tree/
4 “Introduction to Algorithms” (MIT Press), 3-cü nəşr, səhifə 152
5 “Introduction to Algorithms” (MIT Press), 3-cü nəşr, səhifə 151
6 http://www.techiedelight.com/introduction-priority-queues-using-binary-heaps/
7 “Introduction to Algorithms” (MIT Press), 3-cü nəşr, səhifə 152
8 “Bilişim matematiği”, T.R.Çölkesen, səhifə 232
9 “Introduction to Algorithms” (MIT Press), 3-cü nəşr, səhifə 287
10 www.cs.rochester.edu/~gildea/csc282/slides/C12-bst.pdf
11 www.cs.cmu.edu/~adamchik/15-121/lectures/Trees/trees.html
12 https://www.cs.swarthmore.edu/~newhall/unixhelp/Java_bst.pdf
13 https://en.m.wikipedia.org/wiki/Recursion_(computer_science)