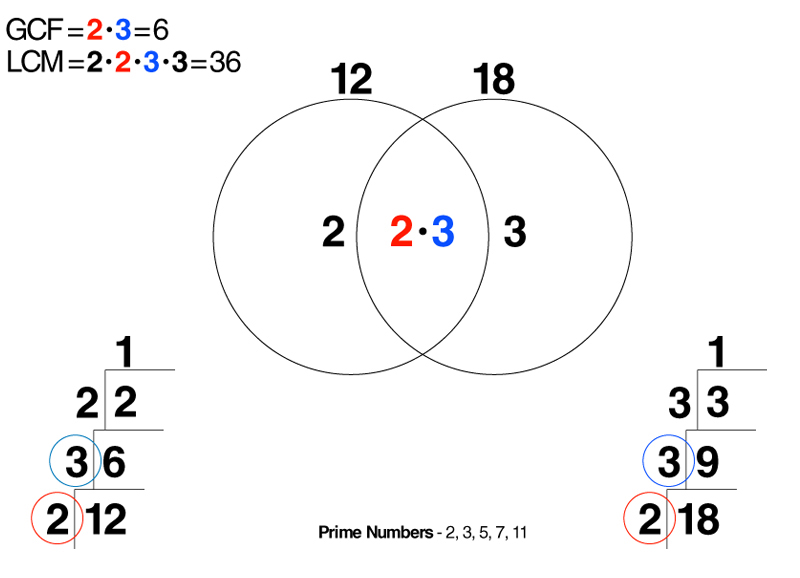
ƏBOB və ƏKOB tapılması. Evklid alqoritmi

ƏBOB və ƏKOB-un tapılmasını hələ məktəb vaxtında öyrənmişik. Qısaca yadımıza salaq. Tutaq ki, ƏBOB(18, 12) və ƏKOB(18, 12)-ni tapmalıyıq. İlk öncə ədədləri sadə vuruqlarına ayırırdıq:

ƏBOB-u tapmaq üçün ortaq sadə vuruqları bir-birinə vururduq:

• ƏBOB(18, 12) = 2 x 3;

ƏKOB-u tapmaq üçün həmin ədədlərdən biri götürülürdü və digərində olub onda olmayan sadə vuruqlara vurulurdu:

• ƏKOB(18, 12) = 2 x 3 x 3 x 2;

Aşağıdakı şəkildə daha aydın qeyd olunub:

Amma kodlaşdırmaq baxımından bu üsul nisbətən daha “maliyətli” hesab olunur. “Maliyətli” sözü hazırda oxuduğum “Bilişim matematiği” kitabında çox istifadə olunur, əsasən hər hansı bir prosesin icrası üçün yerinə yetiriləcək əməliyyatların sayı, sərf ediləcək zaman, yaddaşdan zəbt ediləcək yer və s. anlamına gəlir.

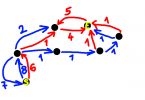
Kodlaşdırmada ƏBOB-un tapılması üçün Evklid alqoritmindən istifadə edilir. Çünki yuxarıda qeyd edilən üsula nisbətən az “maliyyətli”dir və kodlaşdırılması da çox rahatdır. Bu yanaşmada MOD (qalığın alınması) operatorundan istifadə edilir. “Bilişim matematiği” kitabında bu alqoritmin izahı və kodlaşdırılması verilib, amma açığı nə izah, nə də kod xoşuma gəlmədi. Play Store`dan yüklədiyim Algorithms: Explained&Animated mobil tətbiqində bu alqoritm animasiyalı şəkildə çoox gözəl izah edilib. Aşağıdakı şəkil də həmin izahdan bir screenshot-dur, ƏBOB(1112, 695)-in necə tapılmasını göstərir:

Şəkildən artıq hər şey aydın görünür, amma qısaca izahını belə verə bilərik:

1. Böyük ədəd (1112) kiçik ədədə (695) bölünür və qalığı (417) alınır;
2. Kiçik ədəd (695) alınmış qalığa (417) bölünür və qalığı (278) alınır;
3. Bir öncəki qalıq (417) son qalığa (278) bölünür və qalığı alınır… və bu proses qalıq sıfır olanadək davam edir;
4. Qalıq sıfır olduqda sıfırdan öncəki son qalıq (139) ən böyük ortaq bölən hesab edilir.

ƏBOB-un tapılmasını java`da kodlaşdırmamışdan öncə ƏKOB-un da daha rahat şəkildə tapılmasına baxaq. Belə bir sadə riyazi qanunauyğunluq var; 2 ədədin hasili onların ƏBOB-u ilə ƏKOB-unun hasilinə bərabərdir:

• a x b = ƏBOB(a, b) x ƏKOB(a, b)

Bu yanaşmadan yola çıxsaq, ƏBOB-u tapdıqdan sonra ƏKOB-u rahat şəkildə tapa bilərik. İndi isə ƏBOB ilə ƏKOB-un tapılmasını Java’da kodlaşdıraq:

package az.mm.algoritms;

import java.util.Scanner;

public class Evklid {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int a = sc.nextInt(), b = sc.nextInt();
        System.out.println("ƏBOB: " + ebob(a, b));
        System.out.println("ƏKOB: " + ekob(a, b));
    }

    static int ebob(int a, int b) {
        if (a % b == 0) return b;
       return ebob(b, a%b);
    }

    static int ekob(int a, int b) {
        return a*b / ebob(a, b);
    }
}

Göründüyü kimi ebob() metodu rekursiv metoddur, yəni özü-özünü çağırır. Sağlıq olsun, rekursiv metodlar haqqında da ayrıca məqalə yazmağı planlaşdırıram İnşallah.

Ümid edirəm faydalı olmuşdur. Uğurlar!