İntervülərin birində 1-dən 10-a kimi ədədlərin rekursiv metod vasitəsilə 10, 9, 8, .., 2, 1 şəklində çap edilməsi tapşırığı verilmişdi. Orada tam olaraq necə yazdığımı xatırlamıram, amma təxminən belə bir şey idi:
static void printDesc(int a) {
System.out.print(a + " ");
if (a > 1) printDesc(a - 1);
}
Sonra isə eyni tapşırığın tərsini 1, 2, 3, .. , 9, 10 şəklində çap edilməsini yazmağım istənildi. Təxminən 5 dəqiqə fikirləşdim, amma yaza bilmədim. Yaxşı ki, çox fikirləşməmişdim, çünki yaza bilməyəcəkdim 🙂 Tapşırığı yaza bilmək üçün rekursiv metodlarla bağlı praktik təcrübə lazım idi, bütün işin məğzi rekursiv metodun təbiətindən irəli gələn bir şey idi. Həmin tapşırığı yazmaq üçün yuxarıda yazdığım kodda sadəcə bircə dəyişiklik etmək kifayət edirdi; print əmri ilə if şərtinin yerlərini dəyişdirmək:
package az.mm.algoritms;
public class Recursion {
public static void main(String[] args) {
printDesc(10);
System.out.println();
printAsc(10);
}
static void printDesc(int a) {
System.out.print(a + " ");
if (a > 1) printDesc(a - 1);
}
static void printAsc(int a) {
if (a > 1) printAsc(a - 1);
System.out.print(a + " ");
}
}
Output:
10 9 8 7 6 5 4 3 2 1
1 2 3 4 5 6 7 8 9 10
printAsc(int ) metodu aşağıdakı ardıcıllığa uyğun olaraq işləyir, ona görə də əvvəlcə 1, son olaraq isə 10 çap olunur:
main
printAsc(10)
printAsc(9)
printAsc(8)
printAsc(7)
printAsc(6)
printAsc(5)
printAsc(4)
printAsc(3)
printAsc(2)
printAsc(1)
stop recursion
print 1
print 2
print 3
print 4
print 5
print 6
print 7
print 8
print 9
print 10
Aşağıdakı paraqraf Quick Sort mövzusunu oxuyanda təsadüfən qarşıma çıxdı, tam da bizim yuxarıdakı sualın cavabıdır:
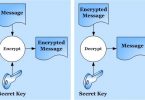
Compilers usually execute recursive procedures by using a stack that contains pertinent information, including the parameter values, for each recursive call. The information for the most recent call is at the top of the stack, and the information for the initial call is at the bottom. Upon calling a procedure, its information is pushed onto the stack; when it terminates, its information is popped.
“Introduction to Algorithms”, 3-cü nəşr, səhifə 188
Paraqrafdan çıxan nəticəyə görə bu stack yaddaş ilə əlaqəli məsələdir. Metod rekursiv olaraq təkrar-təkrar çağırıldıqca həmin metoda ötürülən parametrlər stack yaddaşa əlavə edilir. Rekursiya bitdikdən sonra həmin parametrlərə müraciət edildikdə isə stack`ə ən son əlavə edilən ən birinci çağırılır (çıxarılır). Yəni loru dildə belə misal göstərə bilərik. Elə hesab edin ki, siz stolun üstünə kitablarınızı bir-bir üst-üstə yığmağa başlayırsınız. Sonra stolun üzərindən bir-bir götürüb rəfə qoyursunuz. Kitablarınızı götürərkən qoyduğunuz ardıcıllığın tam tərsi baş verir. İlk qoyduğunuz kitablar altlarda qalır, son qoyduğunuz kitablar isə üstlərdə. Və beləliklə əvvəlcə son qoyduğunuz kitabları və sonda isə ilk qoyduğunuz kitabları götürürsünüz. Yəni, bir sözlə stack öz işində LIFO (last-in, first-out) siyasətini tətbiq edir1.
Əlavə. printDesc(int ) metodu “tail recursion”, printAsc(int ) metodu isə “non-tail recursion” hesab edilir. Nə deməkdir bu?
Əgər rekursiv çağrı metodun sonuncu sətrində olarsa və həmin sətirdə başqa heç bir əməliyyat olmazsa, bu “tail recursion”, digər hallarda isə “non-tail recursion” adlanır. Məsələn, aşağıda görəcəyiniz Faktorial, String reverse üçün yazılmış metodlarda rekursiv çağrı sonuncu sətirdə olsa da tail recursion hesab edilmir, çünki həmin sətirdə əlavə əməliyyatlar da gedir. Amma Evklid alqoritmi üçün yazılmış ebob() metodu tail recursion hesab edilir.
Bəs metodun tail recursion yaxud non-tail recursion olmasının nə önəmi var?
Tail recursion performans baxımından non-tail recursion-dan daha yaxşıdır. Çünki modern kompilyatorlar tail recursion-u təyin edə və kodu optimallaşdıra bilirlər. Tail recursionun əsas özəlliyi odur ki, dəyərlərin stack yaddaşa əlavə edilməsinə ehtiyac yoxdur. Bu səbəbdən də yaddaşa və vaxta qənaət edilir2.
Rekursiv metodların əhəmiyyəti nədir, nə üçün istifadə edilir?
Bəzi alqoritmlər quruluş baxımından rekursiv struktura çox yaxındır və onların rekursiv metodlar istifadə olunaraq kodlaşdırılması həm rahat, həm də oxunaqlılıq baxımından anlaşıqlıdır. Həmçinin rekursiya əsasən “divide and conquer” yanaşması tətbiq edilən alqoritmlərdə istifadə olunur ki, bunlardan da ən klassiki Merge Sort alqoritmidir. Həmin alqoritmdə rekursiyanın necə işləməsini başa düşmək nisbətən daha çətin olduğuna görə bu yazımızda daha sadə nümunələrə baxacağıq. Merge Sort ilə bağlı yazımızda isə həmin məsələni daha detallı müzakirə edərik.
Faktorialın hesablanması
5! = 5 * 4 * 3 * 2 * 1
İndi isə kodlaşdırılmasına baxaq:
package az.mm.algoritms;
public class Factorial {
public static void main(String[] args) {
System.out.println(factorial(5)); // 120
}
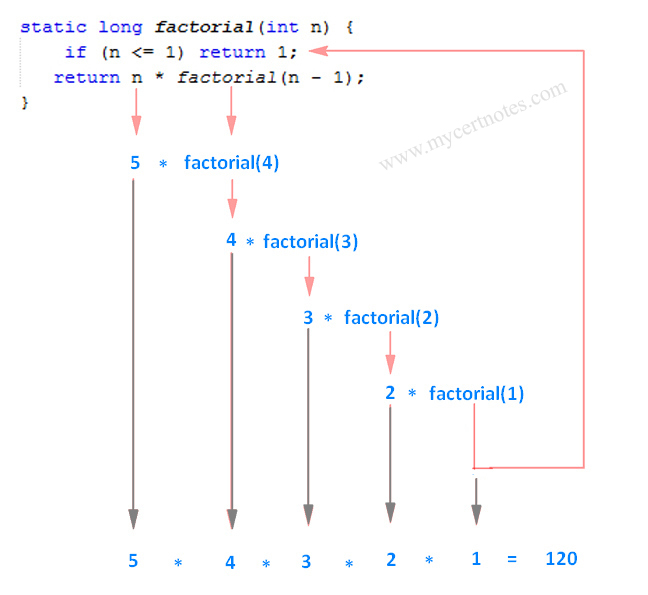
static long factorial(int n) {
if (n <= 1) return 1;
return n * factorial(n - 1);
}
}
Burada factorial(int ) metodunun necə işləməsi daha açıqlayıcı olsun deyə paint`də balaca cızma-qara etmişəm, ona baxaraq bu metodun necə işləməsini daha aydın başa düşə bilərsiniz:
Fibonaççi ədədlərinin tapılması
Fibonaççi ədədləri ilə bağlı internetdə bir xeyli yazı mövcuddur, ona görə də çəx dərinə getməyəcəyik. Qısaca izah verib kodunu yazacağıq.
Fibonaççi ədədləri müəyyən qanunauyğunluğa görə düzülmüş ədədlərin ardıcıllığıdır. Ardıcıllıqda birinci və ikinci ədədlər “1”-dir (bəzi mənbələrdə “0” və “1”). Hər növbəti ədəd özündən əvvəlki ilk iki ədədin cəminə bərabərdir:
Fn = Fn-1 + Fn-2
Ardıcıllığa baxaq:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...
İndi isə Java`da rekursiv şəkildə kodlaşdırılmasına baxaq:
package az.mm.algoritms;
import java.util.Scanner;
public class FibonacciNumbers {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for (int i = 1; i <= n; i++)
System.out.print(fibonacci(i) + " ");
}
public static int fibonacci(int n) {
if (n == 1 || n == 2) return 1;
return fibonacci(n-1) + fibonacci(n-2);
}
}
Bu kodda rekursiyanın necə işləməsini başa düşmək üçün ardıcıllıqdan nümunə bir ədəd götürək və əyani olaraq izah edək. Nümunə üçün Fibonaççi ardıcıllığının 6-cı ədədini tapaq. Yuxarıdakı ardıcıllıqdan görürük ki, 6-cı ədəd 8-dir. Bəs 8 ədədi bu koddan necə alınır?
6-cı sırada dayanan ədədi tapmaq üçün koddan çıxan düstur belədir:
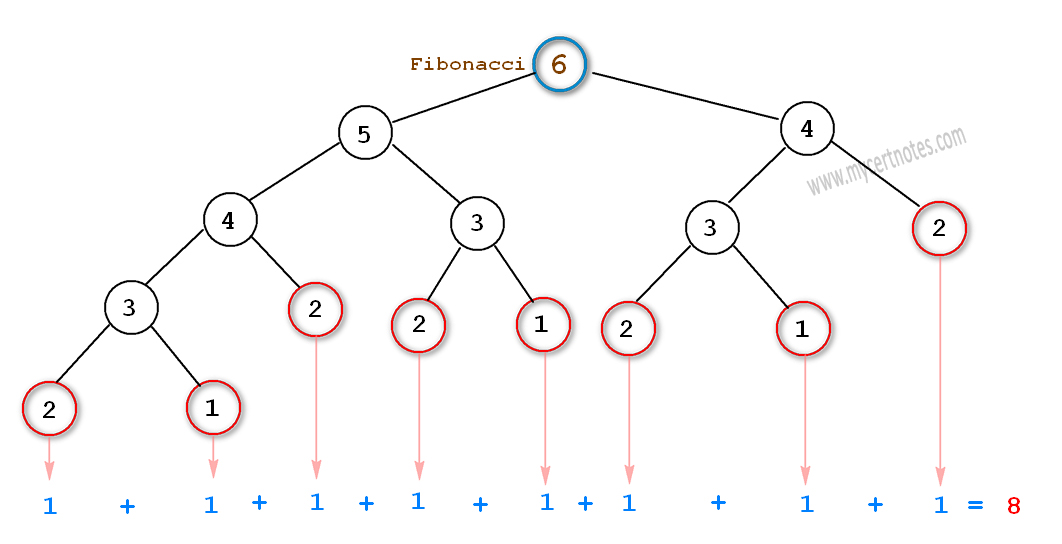
fibonacci(6) = fibonacci(5) + fibonacci(4)
Rekursiv metodların ən vacib tərkib elementlərindən biri rekursiyanın bitməsini bildirən şərtdir. Bizim kodumuzda da n=1 və yaxud n=2 olduqda metod sonlanır. Bu şərtə görə fibonacci(5) və fibonacci(4) də öz növbəsində fibonacci(2) və ya fibonacci(1) olanadək parçalanacaqlar. Belə məqamda qrafik görüntü izah üçün daha effektiv olur. Paint`lə aram elə də yaxşı olmasa da izah üçün bir şəkil hazırladım, ümid edirəm yetərli olar:
fibonacci(7) üçün bu qrafiki özünüz çəkə bilərsiniz, sonda görəcəksiniz ki, “1” və “2” düyünlərinin sayı 13 ədəd olacaqdır.
Fibonaççi ədədlərinin tapılmasının dinamik proqramlaşdırma ilə çox maraqlı həll variantı da var, bir az əlavə yaddaş (space complexity) istifadə edilsə də performans (time complexity) baxımından kodu xeyli yaxşılaşdırmaq mümkündür.
Evklid alqoritmi
Evklid alqoritmi ilə əlaqəli blogda ayrıca məqalə mövcuddur, burada qısaca koduna baxaq:
package az.mm.algoritms;
import java.util.Scanner;
public class Evklid {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int a = sc.nextInt(), b = sc.nextInt();
System.out.println("ƏBOB: " + ebob(a, b));
System.out.println("ƏKOB: " + ekob(a, b));
}
static int ebob(int a, int b) {
if (a % b == 0) return b;
return ebob(b, a % b);
}
static int ekob(int a, int b) {
return a * b / ebob(a, b);
}
}
String reverse
Sözlərin və ya mətnlərin tərsinə çevirilməsi üçün bir neçə yol mövcuddur ki, onlardan da ən rahatı StringBuilder classının reverse() metodudur. Ancaq bunu sizin özünüzün yazması istənilə bilər. Dövrün köməkliyi ilə və yaxud rekursiya vasitəsilə bunu edə bilərsiniz. Amma mövzumuz rekursiya olduğu üçün biz rekursiya ilə bağlı nümunəyə baxacağıq:
package az.mm.algoritms.recursion;
public class StringReverse {
public static void main(String[] args) {
System.out.printf("programmer --> %s%n",
new StringBuilder("programmer").reverse());
System.out.printf("programmer --> %s%n%n", reverse("programmer"));
}
public static String reverse(String str) {
if (str.length() == 0) return str;
return reverse(str.substring(1)) + str.charAt(0);
}
}
Output:
programmer --> remmargorp
programmer --> remmargorp
İndi isə keçək izahına. İnternetdə araşdırsanız fərqli cür izahlara rast gələcəksiz. Özüm də fərqli bir prizmadan yanaşdım və koda print ifadələri əlavə etdim, hansı ki, hadisələrin axışının hansı ardıcıllıqla getməsini daha rahat şəkildə görməyə imkan verir. Ümid edirəm, belə daha açıqlayıcı olacaq:
package az.mm.algoritms.recursion;
public class StringReverse {
public static void main(String[] args) {
reverseExplain("programmer");
}
public static String reverseExplain(String str) {
if (str.length() == 0) {
System.out.println("Recursion ends, reverse starts!");
return str;
}
String s = reverseExplain(getSubstring(str)) + getFirstChar(str);
return s;
}
private static char getFirstChar(String str) {
System.out.println(str + " --> " + str.charAt(0));
return str.charAt(0);
}
private static String getSubstring(String str) {
System.out.println(str.substring(1));
return str.substring(1);
}
}
Output:
rogrammer
ogrammer
grammer
rammer
ammer
mmer
mer
er
r
Recursion ends, reverse starts!
r --> r
er --> e
mer --> m
mmer --> m
ammer --> a
rammer --> r
grammer --> g
ogrammer --> o
rogrammer --> r
programmer --> p
Yuxarıda qeyd etmişdik ki, metoda göndərilən parametrlər stack yaddaşa əlavə edilir (PUSH). İlk göndərilən parametr “programmer” sözüdür, ardınca rekursiv olaraq çağırılan reverseExplain(String ) metodu vasitəsilə stack`ə əlavə edilən parametrlər isə output`da çap edilib. Göründüyü kimi sonuncu əlavə edilən dəyər “r”-dir. Rekursiya bitdikdən sonra artıq getFirstChar(String ) metodu çağırılır. Yuxarıda həmçinin qeyd etmişdik ki, stack`ə sonuncu əlavə edilən parametrlər birinci çıxarılır (POP). Koda diqqətlə baxsanız görəcəksiniz ki, reverseExplain(String ) metoduna göndərilən parametrlər həm rekursiyadan əvvəl, həm də sonra print edilir və rekursiyadan sonra print edilmə ardıcıllığı tamamilə birincinin tərsidir. “r” stack`ə sonuncu əlavə edilsə də birinci çıxarılır.
Rekursiv metodların müsbət və mənfi tərəfləri
Müsbət:
Daha az kodla və daha anlaşıqlı şəkildə problemi həll etmək mümkündür.
Mənfi:
Rekursiv metodlar stack yaddaş istifadə edir və stack yaddaşın həcmi limitlidir. Rekursiv çağrıların sayı çox olarsa, stack yaddaş dola və StackOverflowError baş verə bilər. Həmçinin rekursiyanın bitməsini bildirən şərti təyin edərkən də diqqətli olmaq lazımdır, şərt düzgün təyin edilməzsə, rekursiya tamamlanmaya və nəticədə yenə StackOverflowError baş verə bilər.
Haşiyəyə çıxaraq bir məqamı da qeyd edim. Bəzən düzgün kodlaşdırma edilmədikdə proqramlaşdırma dilinin sintaksisi ilə əlaqədar olaraq sonsuz rekursiv çağrılar baş verə bilər ki, bu da öz növbəsində StackOverflowError`a səbəb olacaq. Belə məqamlarda diqqətli olmaq və təbii ki, proqramlaşdırma dilinin əsaslarını daha yaxşı öyrənmək, mənimsəmək lazımdır. Java’da yazılmış aşağıdakı kod parçası buna nümunədir:
package az.mm.algoritms.recursion;
public class Recursion {
private Recursion r1 = new Recursion();
private int a = 5;
public Recursion() {
r1.a = 3;
}
public static void main(String[] args) {
Recursion r2 = new Recursion();
System.out.println(r2.a);
}
}
Bu yazımızın da sonuna gəldik. Mövzu ilə bağlı yeni, maraqlı faktlar qarşıma çıxdıqca yazı təkmilləşdiriləcəkdir. Ümid edirəm, faydalı olmuşdur. Uğurlar!
Github link:
https://github.com/mmushfiq/Recursion
1 “Introduction to Algorithms” (MIT Press), 3-cü nəşr, səhifə 232
