Alqoritm oxuduğum dönəmlərdə bloglarda, youtube kanallarında paylaşılan izahların altında tez-tez belə şərhlərə rast gəlirdim:
“Alqoritmi çox gözəl izah etmisiz. Əla, pakizə! Amma bu nə işə yarıyır?”
İnsanları daha çox alqoritmlərin real problemlər üzərində tətbiqi maraqlandırır. Blogda bu səpkidə daha öncə bir məqalə paylaşmışam, səhm alqı-satqısı məsələsində Kadane alqoritminin necə tətbiq edilməsi ilə bağlı. Bu dəfə paylaşmaq istədiyim məsələ isə daha maraqlıdır 🙂 Bu məsələ “Introduction to Algorithms” (MIT Press) kitabında “Graph Algorithms” bölməsini oxuyarkən qarşıma çıxdı, “Single-Source Shortest Paths” mövzusunun sonunda tapşırıq kimi qoyulmuşdu1:
24-3 Arbitrage
Arbitrage is the use of discrepancies in currency exchange rates to transform one unit of a currency into more than one unit of the same currency. For example, suppose that 1 U.S. dollar buys 49 Indian rupees, 1 Indian rupee buys 2 Japanese yen, and 1 Japanese yen buys 0.0107 U.S. dollars. Then, by converting currencies, a trader can start with 1 U.S. dollar and buy
49 x 2 x 0.0107 = 1.0486U.S. dollars, thus turning a profit of4.86percent.Suppose that we are given n currencies
c1, c2, ..., cnand ann x ntable R of exchange rates, such that one unit of currencycibuysR[i, j]units of currencycj.a. Give an efficient algorithm to determine whether or not there exists a sequence of currencies
{ci1, ci2, ..., cik}such that
R[i1, i2] * R[i2, i3] ... R[ik-1, ik] * R[ik, i1] > 1.
Analyze the running time of your algorithm.b. Give an efficient algorithm to print out such a sequence if one exists. Analyze the running time of your algorithm.
Arbitraj “risk-free” gəlir hesab edilir, eyni qiymətli kağızların müxtəlif birjalarda eyni vaxtda fərqli qiymətlərə satılmasından yaranır. Yuxarıdakı məsələnin isə qısa izah etsək məğzi belədir:
Sizdə 100 AZN var, onu satıb 62 USD alırsınız. Sonra 62 USD-ni satıb 57 EUR alırsınız. Sonda 57 EUR-u satıb 105 AZN əldə edirsiniz. Yəni, 100 AZN ilə başlayırsınız, 3 çevirmədən sonra isə 105 AZN pulunuz olur, əlavə 5 manat qazanc.
Yuxarıdakı tapşırıqda tələb olunan isə bu məsələnin alqoritmini qurmaqdır.
Bir köhnə iqtisadçı kimi məsələ çox diqqətimi çəkdi və rəhmətlik Nəsibə Zeynalova demişkən məni çox uzaqlara apardı 🙂 Bununla bağlı bir aydan çox müddət ərzində fasilələrlə 100-dən artıq mənbə – kitab, məqalə, universitet mühazirələri, blog postları, forum müzakirələri, video izahlar və s. oxuyub baxdım. Qraflarla bağlı konkret olaraq mövcud olmayan bir şeyi axtarıb tapmağa çalışırmışam) Sonda konkret olaraq mümkündür ya mümkün deyil onu yenə də təyin edə bilmədim) Amma demək olar istədiyim nəticəni əldə edə bildim, bir-iki nüansı nəzərə almasaq.
Alqoritmin effektiv işlədiyini göstərmək üçün daha maraqlı nümunə olsun deyə bu arbitraj məsələsini yerli banklar üzərində tətbiq etməyi qərara aldım. Aşağıdakı formada nəticəni məqalənin girişində yerləşdirdiyim github linkindən proqramı yükləyib, özünüz test etməklə də əldə edə biləcəksiniz:
Select data:
1 - Excel, 2 - AznToday, 3 - AniMezenne, 4 - Json
1
Select algorithm:
1 - Princeton Bellman-Ford, 2 - Bellman-Ford, 3 - Permutation
3
Currency list: AZN USD EUR GBP RUB TRY
Select base currency from the list:
AZN
Select currencies which you want:
USD EUR GBP RUB TRY
Date: 2017-09-07
USD EUR GBP RUB TRY AZN
USD 1.0000 -> 0.8528 -> Bank Melli İran 0.7622 -> AccessBank 59.2632 -> AccessBank 3.3500 -> PAŞA Bank 1.6970 -> AmrahBank
EUR 1.1964 -> AmrahBank 1.0000 -> 0.9049 -> Nikoil Bank 69.3895 -> AccessBank 3.9960 -> PAŞA Bank 2.0350 -> AmrahBank
GBP 1.3061 -> Gunay Bank 1.0823 -> Gunay Bank 1.0000 -> 75.4807 -> AccessBank 4.3749 -> PAŞA Bank 2.2230 -> Gunay Bank
RUB 0.0172 -> DəmirBank 0.0144 -> DəmirBank 0.0131 -> DəmirBank 1.0000 -> 0.0563 -> Gunay Bank 0.0293 -> Azərpoçt
TRY 0.2882 -> PAŞA Bank 0.2402 -> PAŞA Bank 0.2182 -> PAŞA Bank 16.4983 -> PAŞA Bank 1.0000 -> 0.4900 -> PAŞA Bank
AZN 0.5886 -> NBCBank 0.5076 -> Bank Melli İran 0.4513 -> AccessBank 35.0877 -> AccessBank 1.9940 -> PAŞA Bank 1.0000 ->
Arbitrage 1: (profit - 32.99 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 1032.9949 AZN (AmrahBank)
Arbitrage 2: (profit - 3.16 AZN)
1000.0000 AZN = 451.2635 GBP (AccessBank)
451.2635 GBP = 1003.1588 AZN (Gunay Bank)
Arbitrage 3: (profit - 28.07 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 1028.0702 AZN (Azərpoçt)
Arbitrage 4: (profit - 30.57 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 607.2868 USD (AmrahBank)
607.2868 USD = 1030.5658 AZN (AmrahBank)
Arbitrage 5: (profit - 0.21 AZN)
1000.0000 AZN = 451.2635 GBP (AccessBank)
451.2635 GBP = 589.4000 USD (Gunay Bank)
589.4000 USD = 1000.2118 AZN (AmrahBank)
Arbitrage 6: (profit - 25.65 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 604.3916 USD (DəmirBank)
604.3916 USD = 1025.6526 AZN (AmrahBank)
Arbitrage 7: (profit - 21.44 AZN)
1000.0000 AZN = 588.5815 USD (NBCBank)
588.5815 USD = 501.9375 EUR (Bank Melli İran)
501.9375 EUR = 1021.4429 AZN (AmrahBank)
Arbitrage 8: (profit - 26.31 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 504.3268 EUR (DəmirBank)
504.3268 EUR = 1026.3050 AZN (AmrahBank)
Arbitrage 9: (profit - 21.15 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 459.3567 GBP (Nikoil Bank)
459.3567 GBP = 1021.1500 AZN (Gunay Bank)
Arbitrage 10: (profit - 24.84 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 461.0180 GBP (DəmirBank)
461.0180 GBP = 1024.8430 AZN (Gunay Bank)
Arbitrage 11: (profit - 22.02 AZN)
1000.0000 AZN = 588.5815 USD (NBCBank)
588.5815 USD = 34881.1995 RUB (AccessBank)
34881.1995 RUB = 1022.0191 AZN (Azərpoçt)
Arbitrage 12: (profit - 32.04 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 35223.0831 RUB (AccessBank)
35223.0831 RUB = 1032.0363 AZN (Azərpoçt)
Arbitrage 13: (profit - 23.89 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 504.3268 EUR (DəmirBank)
504.3268 EUR = 603.3539 USD (AmrahBank)
603.3539 USD = 1023.8916 AZN (AmrahBank)
Arbitrage 14: (profit - 18.15 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 459.3567 GBP (Nikoil Bank)
459.3567 GBP = 599.9706 USD (Gunay Bank)
599.9706 USD = 1018.1501 AZN (AmrahBank)
Arbitrage 15: (profit - 21.83 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 461.0180 GBP (DəmirBank)
461.0180 GBP = 602.1405 USD (Gunay Bank)
602.1405 USD = 1021.8323 AZN (AmrahBank)
Arbitrage 16: (profit - 29.61 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 35223.0831 RUB (AccessBank)
35223.0831 RUB = 606.7233 USD (DəmirBank)
606.7233 USD = 1029.6094 AZN (AmrahBank)
Arbitrage 17: (profit - 48.88 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 604.3916 USD (DəmirBank)
604.3916 USD = 515.4203 EUR (Bank Melli İran)
515.4203 EUR = 1048.8803 AZN (AmrahBank)
Arbitrage 18: (profit - 22.86 AZN)
1000.0000 AZN = 451.2635 GBP (AccessBank)
451.2635 GBP = 589.4000 USD (Gunay Bank)
589.4000 USD = 502.6356 EUR (Bank Melli İran)
502.6356 EUR = 1022.8634 AZN (AmrahBank)
Arbitrage 19: (profit - 15.36 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 461.0180 GBP (DəmirBank)
461.0180 GBP = 498.9499 EUR (Gunay Bank)
498.9499 EUR = 1015.3630 AZN (AmrahBank)
Arbitrage 20: (profit - 20.26 AZN)
1000.0000 AZN = 588.5815 USD (NBCBank)
588.5815 USD = 34881.1995 RUB (AccessBank)
34881.1995 RUB = 501.3584 EUR (DəmirBank)
501.3584 EUR = 1020.2644 AZN (AmrahBank)
Arbitrage 21: (profit - 24.04 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 604.3916 USD (DəmirBank)
604.3916 USD = 460.6577 GBP (AccessBank)
460.6577 GBP = 1024.0421 AZN (Gunay Bank)
Arbitrage 22: (profit - 28.95 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 607.2868 USD (AmrahBank)
607.2868 USD = 462.8644 GBP (AccessBank)
462.8644 GBP = 1028.9475 AZN (Gunay Bank)
Arbitrage 23: (profit - 9.73 AZN)
1000.0000 AZN = 588.5815 USD (NBCBank)
588.5815 USD = 501.9375 EUR (Bank Melli İran)
501.9375 EUR = 454.2197 GBP (Nikoil Bank)
454.2197 GBP = 1009.7304 AZN (Gunay Bank)
Arbitrage 24: (profit - 14.54 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 504.3268 EUR (DəmirBank)
504.3268 EUR = 456.3818 GBP (Nikoil Bank)
456.3818 GBP = 1014.5368 AZN (Gunay Bank)
Arbitrage 25: (profit - 18.81 AZN)
1000.0000 AZN = 588.5815 USD (NBCBank)
588.5815 USD = 34881.1995 RUB (AccessBank)
34881.1995 RUB = 458.3045 GBP (DəmirBank)
458.3045 GBP = 1018.8110 AZN (Gunay Bank)
Arbitrage 26: (profit - 28.80 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 35223.0831 RUB (AccessBank)
35223.0831 RUB = 462.7966 GBP (DəmirBank)
462.7966 GBP = 1028.7968 AZN (Gunay Bank)
Arbitrage 27: (profit - 54.50 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 607.2868 USD (AmrahBank)
607.2868 USD = 35989.7362 RUB (AccessBank)
35989.7362 RUB = 1054.4993 AZN (Azərpoçt)
Arbitrage 28: (profit - 23.44 AZN)
1000.0000 AZN = 451.2635 GBP (AccessBank)
451.2635 GBP = 589.4000 USD (Gunay Bank)
589.4000 USD = 34929.7068 RUB (AccessBank)
34929.7068 RUB = 1023.4404 AZN (Azərpoçt)
Arbitrage 29: (profit - 20.50 AZN)
1000.0000 AZN = 588.5815 USD (NBCBank)
588.5815 USD = 501.9375 EUR (Bank Melli İran)
501.9375 EUR = 34829.1816 RUB (AccessBank)
34829.1816 RUB = 1020.4950 AZN (Azərpoçt)
Arbitrage 30: (profit - 15.91 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 459.3567 GBP (Nikoil Bank)
459.3567 GBP = 34672.5675 RUB (AccessBank)
34672.5675 RUB = 1015.9062 AZN (Azərpoçt)
Arbitrage 31: (profit - 12.98 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 461.0180 GBP (DəmirBank)
461.0180 GBP = 498.9499 EUR (Gunay Bank)
498.9499 EUR = 596.9212 USD (AmrahBank)
596.9212 USD = 1012.9753 AZN (AmrahBank)
Arbitrage 32: (profit - 11.56 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 504.3268 EUR (DəmirBank)
504.3268 EUR = 456.3818 GBP (Nikoil Bank)
456.3818 GBP = 596.0851 USD (Gunay Bank)
596.0851 USD = 1011.5564 AZN (AmrahBank)
Arbitrage 33: (profit - 25.77 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 35223.0831 RUB (AccessBank)
35223.0831 RUB = 462.7966 GBP (DəmirBank)
462.7966 GBP = 604.4634 USD (Gunay Bank)
604.4634 USD = 1025.7744 AZN (AmrahBank)
Arbitrage 34: (profit - 13.52 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 459.3567 GBP (Nikoil Bank)
459.3567 GBP = 34672.5675 RUB (AccessBank)
34672.5675 RUB = 597.2406 USD (DəmirBank)
597.2406 USD = 1013.5173 AZN (AmrahBank)
Arbitrage 35: (profit - 18.21 AZN)
1000.0000 AZN = 451.2635 GBP (AccessBank)
451.2635 GBP = 34061.6885 RUB (AccessBank)
34061.6885 RUB = 586.7181 USD (DəmirBank)
586.7181 USD = 500.3484 EUR (Bank Melli İran)
500.3484 EUR = 1018.2090 AZN (AmrahBank)
Arbitrage 36: (profit - 44.97 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 461.0180 GBP (DəmirBank)
461.0180 GBP = 602.1405 USD (Gunay Bank)
602.1405 USD = 513.5005 EUR (Bank Melli İran)
513.5005 EUR = 1044.9735 AZN (AmrahBank)
Arbitrage 37: (profit - 14.57 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 604.3916 USD (DəmirBank)
604.3916 USD = 460.6577 GBP (AccessBank)
460.6577 GBP = 498.5599 EUR (Gunay Bank)
498.5599 EUR = 1014.5694 AZN (AmrahBank)
Arbitrage 38: (profit - 9.39 AZN)
1000.0000 AZN = 588.5815 USD (NBCBank)
588.5815 USD = 34881.1995 RUB (AccessBank)
34881.1995 RUB = 458.3045 GBP (DəmirBank)
458.3045 GBP = 496.0132 EUR (Gunay Bank)
496.0132 EUR = 1009.3868 AZN (AmrahBank)
Arbitrage 39: (profit - 21.68 AZN)
1000.0000 AZN = 451.2635 GBP (AccessBank)
451.2635 GBP = 589.4000 USD (Gunay Bank)
589.4000 USD = 34929.7068 RUB (AccessBank)
34929.7068 RUB = 502.0556 EUR (DəmirBank)
502.0556 EUR = 1021.6832 AZN (AmrahBank)
Arbitrage 40: (profit - 27.99 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 35223.0831 RUB (AccessBank)
35223.0831 RUB = 606.7233 USD (DəmirBank)
606.7233 USD = 462.4349 GBP (AccessBank)
462.4349 GBP = 1027.9927 AZN (Gunay Bank)
Arbitrage 41: (profit - 22.28 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 504.3268 EUR (DəmirBank)
504.3268 EUR = 603.3539 USD (AmrahBank)
603.3539 USD = 459.8668 GBP (AccessBank)
459.8668 GBP = 1022.2839 AZN (Gunay Bank)
Arbitrage 42: (profit - 36.85 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 604.3916 USD (DəmirBank)
604.3916 USD = 515.4203 EUR (Bank Melli İran)
515.4203 EUR = 466.4207 GBP (Nikoil Bank)
466.4207 GBP = 1036.8532 AZN (Gunay Bank)
Arbitrage 43: (profit - 8.57 AZN)
1000.0000 AZN = 588.5815 USD (NBCBank)
588.5815 USD = 34881.1995 RUB (AccessBank)
34881.1995 RUB = 501.3584 EUR (DəmirBank)
501.3584 EUR = 453.6956 GBP (Nikoil Bank)
453.6956 GBP = 1008.5654 AZN (Gunay Bank)
Arbitrage 44: (profit - 51.19 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 607.2868 USD (AmrahBank)
607.2868 USD = 35989.7362 RUB (AccessBank)
35989.7362 RUB = 472.8696 GBP (DəmirBank)
472.8696 GBP = 1051.1892 AZN (Gunay Bank)
Arbitrage 45: (profit - 17.29 AZN)
1000.0000 AZN = 588.5815 USD (NBCBank)
588.5815 USD = 501.9375 EUR (Bank Melli İran)
501.9375 EUR = 34829.1816 RUB (AccessBank)
34829.1816 RUB = 457.6211 GBP (DəmirBank)
457.6211 GBP = 1017.2917 AZN (Gunay Bank)
Arbitrage 46: (profit - 15.22 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 2028.4325 TRY (PAŞA Bank)
2028.4325 TRY = 584.6658 USD (PAŞA Bank)
584.6658 USD = 34649.1434 RUB (AccessBank)
34649.1434 RUB = 1015.2199 AZN (Azərpoçt)
Arbitrage 47: (profit - 14.57 AZN)
1000.0000 AZN = 451.2635 GBP (AccessBank)
451.2635 GBP = 488.3928 EUR (Gunay Bank)
488.3928 EUR = 584.2912 USD (AmrahBank)
584.2912 USD = 34626.9434 RUB (AccessBank)
34626.9434 RUB = 1014.5694 AZN (Azərpoçt)
Arbitrage 48: (profit - 41.80 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 459.3567 GBP (Nikoil Bank)
459.3567 GBP = 599.9706 USD (Gunay Bank)
599.9706 USD = 35556.1532 RUB (AccessBank)
35556.1532 RUB = 1041.7953 AZN (Azərpoçt)
Arbitrage 49: (profit - 21.91 AZN)
1000.0000 AZN = 451.2635 GBP (AccessBank)
451.2635 GBP = 589.4000 USD (Gunay Bank)
589.4000 USD = 502.6356 EUR (Bank Melli İran)
502.6356 EUR = 34877.6166 RUB (AccessBank)
34877.6166 RUB = 1021.9142 AZN (Azərpoçt)
Arbitrage 50: (profit - 23.66 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 607.2868 USD (AmrahBank)
607.2868 USD = 462.8644 GBP (AccessBank)
462.8644 GBP = 34937.3288 RUB (AccessBank)
34937.3288 RUB = 1023.6637 AZN (Azərpoçt)
Arbitrage 51: (profit - 4.55 AZN)
1000.0000 AZN = 588.5815 USD (NBCBank)
588.5815 USD = 501.9375 EUR (Bank Melli İran)
501.9375 EUR = 454.2197 GBP (Nikoil Bank)
454.2197 GBP = 34284.8225 RUB (AccessBank)
34284.8225 RUB = 1004.5453 AZN (Azərpoçt)
Arbitrage 52: (profit - 9.22 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 604.3916 USD (DəmirBank)
604.3916 USD = 515.4203 EUR (Bank Melli İran)
515.4203 EUR = 2059.6256 TRY (PAŞA Bank)
2059.6256 TRY = 1009.2165 AZN (PAŞA Bank)
Arbitrage 53: (profit - 8.88 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 461.0180 GBP (DəmirBank)
461.0180 GBP = 2016.8964 TRY (PAŞA Bank)
2016.8964 TRY = 581.3407 USD (PAŞA Bank)
581.3407 USD = 495.7626 EUR (Bank Melli İran)
495.7626 EUR = 1008.8770 AZN (AmrahBank)
Arbitrage 54: (profit - 12.03 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 2028.4325 TRY (PAŞA Bank)
2028.4325 TRY = 584.6658 USD (PAŞA Bank)
584.6658 USD = 34649.1434 RUB (AccessBank)
34649.1434 RUB = 455.2556 GBP (DəmirBank)
455.2556 GBP = 1012.0331 AZN (Gunay Bank)
Arbitrage 55: (profit - 5.81 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 459.3567 GBP (Nikoil Bank)
459.3567 GBP = 2009.6284 TRY (PAŞA Bank)
2009.6284 TRY = 579.2458 USD (PAŞA Bank)
579.2458 USD = 34327.9372 RUB (AccessBank)
34327.9372 RUB = 1005.8086 AZN (Azərpoçt)
Arbitrage 56: (profit - 3.87 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 2028.4325 TRY (PAŞA Bank)
2028.4325 TRY = 442.6328 GBP (PAŞA Bank)
442.6328 GBP = 578.1273 USD (Gunay Bank)
578.1273 USD = 34261.6497 RUB (AccessBank)
34261.6497 RUB = 1003.8663 AZN (Azərpoçt)
Arbitrage 57: (profit - 5.46 AZN)
1000.0000 AZN = 35087.7193 RUB (AccessBank)
35087.7193 RUB = 461.0180 GBP (DəmirBank)
461.0180 GBP = 602.1405 USD (Gunay Bank)
602.1405 USD = 513.5005 EUR (Bank Melli İran)
513.5005 EUR = 2051.9541 TRY (PAŞA Bank)
2051.9541 TRY = 1005.4575 AZN (PAŞA Bank)
Arbitrage 58: (profit - 13.69 AZN)
1000.0000 AZN = 507.6142 EUR (Bank Melli İran)
507.6142 EUR = 607.2868 USD (AmrahBank)
607.2868 USD = 35989.7362 RUB (AccessBank)
35989.7362 RUB = 472.8696 GBP (DəmirBank)
472.8696 GBP = 2068.7457 TRY (PAŞA Bank)
2068.7457 TRY = 1013.6854 AZN (PAŞA Bank)
Bu mövzu ilə bağlı minimum 25-30 A4 səhifə məqalə yazmaq olar, amma buna həm səbr, həm də vaxt lazımdır. Ona görə də hazırladığım proqramın source kodlarını məqalənin əvvəlində paylaşdım və bu məqalədə də orada toxunduğum mövzulara qısa-qısa şərh verib ümumi məsələnin nədən getdiyi barədə məlumat verməyə çalışacam. Kimə maraqlı olarsa, proqramın source kodlarına github`dan baxa və ya yükləyib öz kompyuterində test edə bilər.
Problemin qraflar üzərində tətbiqi ilə bağlı qısa məlumat
Deməli, bu alqoritmik tapşırıq Qraflarda “Short paths” alqoritmləri mövzusunda verilmişdi, ona görə də tapşırığı görəndə ağlıma ilk gələn o oldu ki, çox güman bu tapşırıq həmin alqoritmlərdən biri ilə həll edilməlidir. Kitabda həmin bölmədə qeyd olunan əsas “Short paths” alqoritmləri bunlardır:
- Dijkstra;
- Bellman-Ford;
- Floyd-Warshall.
Dijkstra və Bellman-Ford alqoritmləri “Single-Source” hesab edilir, yəni qraf üzərində bir təpə (vertex) seçilir və həmin təpədən digər bütün təpələrə qədər olan ən qısa yol tapılır. Floyd-Warshall alqoritmi isə “All-Pairs Shortest Paths” üçün istifadə edilir, yəni qraf üzərində istənilən iki təpə arasında ən qısa məsafəni göstərir. Arbitraj məsələsi üçün bizə “Single-Source” alqoritm lazım olacaq, ancaq hansı?
Əvvəlcə qeyd edək ki, arbitraj üçün istifadə edəcəyimiz qraf yönlü (directed) və ağırlıqlı (weighted) olacaq. Bu qraf üzərində Dijkstra və Bellman-Ford demək olar məzmunca eyni işi görürlər, amma Dijkstra “greedy” alqoritm olduğundan performans baxımından Bellman-Ford`dan daha sürətlidir. Bu iki alqoritm arasında əsas fərq isə odur ki, Dijkstra alqoritmini “negative-weighted” qraflarda istifadə etmək mümkün deyil. Bellman-Ford alqoritmi isə “negative-weighted” qraflar üçün istifadə edildikdə düzgün nəticə verir, amma bir şərtlə ki, həmin qrafda “negative-cycle” olmasın (bu halda da düzgün nəticə verə bilər amma müəyyən optimallaşdırmalar aparılmaqla). “Negative-cycle” nədir? – bax işin bütün canı bu iki sözdən ibarət termindədir 🙂
Aha, aydınlaşdırdıq ki, “negative-cycle”-dan istifadə edəcəyik və bunun üçün də Bellman-Ford alqoritmini tətbiq edəcəyik. Amma “negative-cycle” nə olan şeydir, bunu problemin həllinə necə tətbiq edəcəyik? – bunları yaxşı başa düşmək üçün bir haşiyəyə çıxmalıyıq.
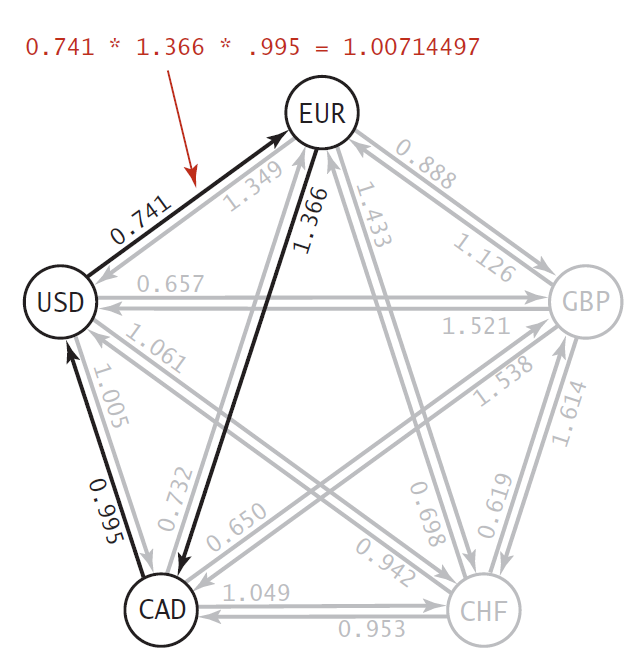
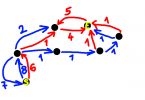
Deməli bu məsələni araşdırarkən bu problemin həlli ilə bağlı ən tutarlı izaha Princeton Universiteti professorları Robert Sedgewick və Kevin Wayne`nin “Algorithms” kitabında rast gəldim. Mürəkkəb formada da olsa Java`da kodlaşdırılması da var hətta. Bütün araşdırmalarıma həmin kitab üzərindən başladım və kod nümunələrini oxuyaraq məsələnin həllini başa düşməyə çalışdım. Ümumiyyətlə, bu kitab alqoritmlə bağlı çox gözəl kitabdır, kod nümunələri də Java`da yazılıb və kodlara baxdıqca heyran qalmamaq mümkün deyil. Aşağıdakı şəkil arbitraj ilə bağlı həmin kitabdan alınmış screenshot`dur2:
Arbitraj məsələsini qraf üzərində təsvir etsək yuxarıdakı mənzərə alınacaq: valyutalar “vertex”, bir valyutadan digər valyutaya çevrilmənin dəyərini (rate/weight) göstərən oxlar isə “edge” olacaq. Yuxarıda tünd qara rənglərlə göstərilmiş oxlar USD –> EUR –> CAD –> USD arbitraj imkanını göstərir, yəni bir valyutadan başlayırıq, çevrə cızaraq yenidən həmin valyutaya qayıdırıq. Və hər addımda da çevrilmə dəyərlərini bir-birinə vururuq. Əgər alınan nəticə 1-dən böyükdürsə, deməli arbitraj imkanı var.
İndi isə işin ən maraqlı tərəflərindən biri gəlir. Yuxarıda qeyd edilən hesablamanı riyazi düstur şəklinə salsaq aşağıdakı bərabərsizlik alınacaq:
R[i1, i2] * R[i2, i3] * ... * R[ik-1, ik] * R[ik, i1] > 1
Yəni bu bərabərsizlik ödənilirsə, arbitraj imkanı var deməkdir. İndi isə bu bərabərsizliyi bir-iki riyazi çevirmə fəndi istifadə edərək fərqli şəklə gətirəcəyik3:
(1) R[i1, i2] * R[i2, i3] * ... * R[ik-1, ik] * R[ik, i1] > 1
(2) 1/R[i1, i2] * 1/R[i2, i3] * ... * 1/R[ik-1, ik] * 1/R[ik, i1] < 1
(3) lg 1/R[i1, i2] + lg 1/R[i2, i3] + ... + lg 1/R[ik-1, ik] + lg 1/R[ik, i1] < 0
(4) -lg R[i1, i2] + (-lg R[i2, i3]) + ... + (-lg R[ik-1, ik]) + (-lg R[ik, i1]) < 0
(1) və (4) bərabərsizlikləri bir-birinə ekvivalentdir. Bəs sual oluna bilər ki, (4) bərabərsizliyi bizim nəyimizə lazımdır? Yuxarıda “negative cycle” termini işlətmişdik, gəlin onu açaq: çevrə (cycle) yaradan vertex`lərin ağırlıqlarının (weight) cəmi sıfırdan kiçik olarsa, həmin çevrə neqativ çevrə və ya öz orijinal termini ilə desək “negative cycle” adlanır. Deməli qrafda mövcud olan hər “negative cycle” yeni bir arbitraj imkanı deməkdir. “Negative cycle” mövcud olması üçün də ilk növbədə “weight” dəyərləri arasında mütləq mənfi ədədlər olmalıdır. Valyuta arası çevrilmələrdə mənfi dəyər yoxdur, ona görə də bu bərabərsizliyi tətbiq etmək üçün ilk öncə valyutalararası çevrilmələrin dəyərlərinin loqarifmini alıb, mənfi ədədə çevirib sonra qraf üzərində tətbiq edəcəyik.
Əslində Bellman-Ford alqoritminin ana məqsədi “negative cycle” tapmaq deyil. Bu alqoritm “short path”-i hesablayır. Sadəcə əgər qraf “negative weighted” qrafdırsa, sonda mütləq “negative cycle”un olub olmamasını “detect” edir. Əgər “negative cycle” yoxdursa, hesablanmış “short path”ları göstərir, yox əgər “negative cycle” varsa, bildirir ki, əldə edilmiş nəticə effektiv deyil və alqortimi sonlandırır. Çünki “negative cycle” mövcuddursa, (vertex-1) sayda “relax”dan sonra sonsuza doğru həmişə ən kiçik path mövcuddur. Bizə isə öz problemimizin həlli üçün sırf “negative cycle” lazımdır, amma bundan ötrü öncə alqoritm ənənəvi qaydada işləməli və “relax” edilməlidir. Yuxarıda da qeyd etdiyim kimi bu terminlərin izahına geniş yer verməyəcəm, yoxsa mövzu uzana-uzana gedəcək, internetdə kifayət qədər faydalı resurs mövcuddur. Sadəcə Princeton universiteti mühazirələrindən birinin slaydını qoyuram bura, Bellman-Ford alqoritminin hesablanmasını addım-addım göstərir, ümumi təsəvvür olsun deyə baxa bilərsiniz:
https://algs4.cs.princeton.edu/lectures/44DemoBellmanFord.pdf
Proyektin ümumi strukturu və istifadə edilən alqoritmlər
İndi isə proyektin ümumi strukturu və necə işləməsi ilə bağlı müəyyən məlumatları qeyd edəcəm ki, istifadə edərkən təsəvvür olsun:
Proyekti Console Application kimi hazırlamışam ki, istifadə edərkən redaktələr etmək və yenidən yoxlamaq rahat olsun. Maven`ə çevirmək istədim, amma sonda fikrimdən daşındım. Jar`ları bu linkdən yükləyə bilərsiniz. Bu proyekti Netbeans`də yazmışam, əgər kimsə cross-platform özəlliyindən dolayı Maven`ə keçirmək istəsə, yeni Maven proyekti yaradıb package`ləri kopyala bilər. Məqalənin sonunda isə maven`də pom.xml faylına əlavə ediləcək jarların dependency`lərini əlavə edəcəm.
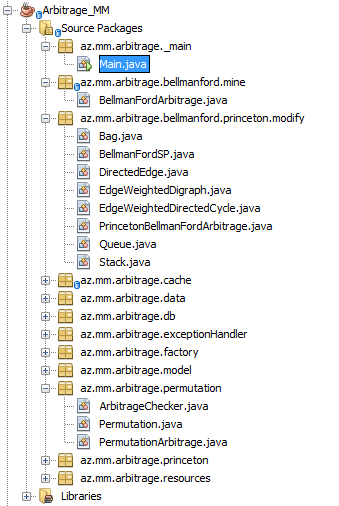
Proyekt strukturuna fikir versəniz problemi həll etmək üçün bir-birindən müstəqil işləyən 3 alqoritmdən istifadə edəcəyik:
- PrincetonBellmanFordArbitrage
- PermutationArbitrage
- BellmanFordArbitrage
1. PrincetonBellmanFordArbitrage – Princeton Universiteti professorları Robert Sedgewick və Kevin Wayne`nin implementasiya etdikləri alqoritmdir. Ümumiyyətlə, bu müəlliflərin “Algoritms” kitablarında yazdıqları kod nümunələri çox xoşuma gəldi, kodları elə optimal yazıblar ki, bir mövzu üçün yazdıqları kodu digər mövzular üçün də istifadə edirlər. Arbitrage üçün hazırladıqları kod cəmi 1 class`dır, amma zəncirvari şəkildə bu kod həmin class`dan əlavə digər 7 class da istifadə edir. Kodun orijinalını az.mm.arbitrage.princeton paketində saxlamışam, az.mm.arbitrage.bellmanford.princeton.modify paketində isə həmin koda müəyyən redaktələr etmişəm. Kodun oxunaqlığı daha rahat olsun deyə Arbitrage üçün lazım olmayan metodları həmin class`lardan silib çıxarmışam. Burada Bellman-Ford alqoritmi klassik implementasiyasından bir az fərqli formada, “Queue-based” əsaslı hazırlanıb. Bu cür hazırlanmasında isə məqsəd peformansı xeyli yaxşılaşdırmaqdır. Bu formada implementasiyanı başa düşmək üçün gərək Bellman-Ford alqoritmini çox yaxşı mənimsəyəsən, mənim də bir az vaxtımı aldı. Deməli, (vertex-1) sayda “relax” etdirməlisən, yəni vetrex`lərin sayı 6-dırsa, 5 dəfə dövr işləyəcək və relax() metodu 5 dəfə çağırılacaq. Amma hansısa dövrdən sonra relax() metodunda heç bir dəyişiklik baş vermirsə, o zaman 5 dəfə relax() metodunu çağırmağa ehtiyac yoxdur, dövrü sonlandırmaq olar. Bu da performansın yaxşılaşmasına kömək edir. Amma bu müəllimlər bir az daha irəli gediblər, Queue istifadə ediblər və dövrdən bir az daha dibə “edge” səviyyəsinə eniblər. Hansı “edge”lərdə dəyişiklik baş verirsə, onları Queue-ya əlavə edib, növbəti “relax”da ancaq “edge”ləri yoxlayırlar.
Qraflarda digər vacib bir məsələ dəyərləri saxlamaq üçün istifadə edilən data strukturdur. Əsasən 2 data strukturdan istifadə edilir:
-
Adjacency Matrix
-
Adjacency List
Bu nümunədə “adjacency list”dən istifadə edilib. Əgər hansı vertex`dən hansı vertex`lərə istiqamət olub olmadığını əvvəlcədən bilmirsinizsə, istifadə etmək üçün bu yaxşı strukturdur. Mən isə öz implement etdiyim nümunədə “adjacency matrix” istifadə etmişəm, səbəbini bir az sonra qeyd edəcəm.
Kodlaşdırma baxımından Princeton nümunəsi çox əladır, amma funksionallıq baxımından belə bir problem var ki, bu nümunə arbitraj imkanı varsa, onlardan sadəcə birini göstərir. “Negative cycle”yə daxil olan valyutaları tapmaq üçün isə qraflar üçün mövcud olan axtarış alqoritmlərindən biri – “depth-first search” alqoritmini istifadə edir. Sonradan araşdırmalarımdan belə başa düşdüm ki, tapılmış bu arbitraj imkanı ən yaxşı olmaya da bilər. Oxuduğum hansısa məqalələrin birində qeyd olunurdu ki, bütün arbitraj imkanlarını tapmaq NP problem sayılır, polinom zamanda tapılması mümkün deyil. Bu şübhələri dəqiqləşdirmək üçün 2-ci alqoritmi fikirləşməyə başladım.
2. PermutationArbitrage – uzun müddət məsələnin içində olduğumdan məntiqi gedişatı tutmuşdum və alqoritmin brute-force variantını implement etməyə qərar verdim. Buna görə permutasiya istifadə elədim. Niyə görə kombinazon yox? Çünki AZN-USD (0.5910) ilə USD-AZN (1.6990) fərqlidir, üzərlərində fərqli dəyərlər saxlayırlar. Bu səbəbdən sıralı olma özəlliyi vacibdir.
Bu alqoritmi implement etdikdən sonra test etdim və gördüm ki, həqiqətən də bu NP problemdir, vertex-lərin (valyutaların) sayı artdıqca “time complexity” təxminən faktorial olaraq artırdı. Amma proyektdə 6 yaxud 7 valyuta istifadə edildiyindən bu bizə problem yaratmırdı. Amma artıq valyuta sayı 10-u keçməyə başlayanda həyəcan təbili çalınmağa başlanacaq)
Performansı nəzərə almasaq bu alqoritmin gözəlliyi ondadır ki, bütün mövcud arbitraj imkanlarını görmək olur və bu alqoritmin əsasında artıq təyin edə bildim ki, 1-ci alqoritm ən yaxşı arbitraj imkanını verir ya yox. Cavab “yox” idi, çünki 1-ci alqoritm tapdığı 1-ci “negative cycle” üzrə arbitraj imkanını göstərir, amma əvəzində performans baxımından çox əla işləyir. Ola bilər ki, sizə sadəcə arbitraj imkanının olub olmaması maraqlı olsun, “hə” yaxud “yox”. Bu zaman 1-ci alqoritm ideal seçimdir.
Bu nümunədə digər bir funksionallıq da əlavə etmişəm, hansı valyutadan başlamaq istəyirsinizsə, onu əvvəlcədən özünüz seçə bilərsiniz. Tutaq ki, əlinizdə AZN yox EUR var, istəyirsiniz ki, EUR ilə başlayan arbitraj imkanlarını görəsiniz. Bu zaman “base currency” olaraq EUR seçirsiniz. Həmçinin arbitraja daxil etmək istəyiniz valyutaların siyahısını da özünüz seçə bilərsiniz (mövcud siyahıdan), əgər TRY daxil olmasını istəmirsinizsə, onu seçmirsiniz. Proqramda valyutaların adlarını console-a daxil edərkən arada boşluq istifadə etməlisiniz.
3. BellmanFordArbitrage – bu alqoritmə əslində daha ehtiyac yox idi, 2-ci alqoritm hər şeyi təfsilatı ilə görməyə imkan verirdi. Amma sırf tərsliyimə görə bu alqoritmin qurbanı oldum, ən çox əziyyət çəkdiyim, ən çox vaxtımı aparan da bu oldu. Bir tərs xüsusiyyətim var, bir şey ki beynimə girdi, 1 ay, 2 ay, lap 5 ay sonra da olmuş olsa onu etməmiş əl çəkə bilmirəm. Lətifəsi məndən uzaq “İt əl çəkdi, motal əl çəkmədi” məsələsi kimi 😀
Uzun sözün qısası, fikirləşdim ki, axı 1-ci alqoritm niyə 1 arbitraj imkanını göstərir ki? Olmazmı ki, bütün “negative cycle”ları tapıb, bu cycle`lər üzrə mövcud bütün arbitrajları göstərək?
Bu sual, bu minvalla yola çıxdım, başımın şişmədiyi gün qalmadı 😀 Bir xeyli mənbə oxudum, araşdırdım, amma heç bir mənbədə bütün “negative cycle”ları göstərməyin mümkün olması ilə bağlı konkret bir fikrə rast gəlmədim. Hərdən də fikirləşirdim ki, əgər mümkün olsaydı, yəqin Princeton nümunəsində nəzərə alardılar, amma yenə də tərslikdən əl çəkməyib səhəri gün yenə araşdırırdım) Hər araşdırdıqca da bu mövzu ilə əlaqəli, ya bu mövzudan kənar xeyli yeni şey oxumuş, bilmiş olurdum. Və sonda başa düşdüm ki, istənilən halda bu üsulla bütün arbitraj imkanlarını tapmaq mümkün olmayacaq, çünki “negative cycle”ların sayı vertex`lərin sayından çox ola bilməz. Alqoritmin fəlsəfəsinə görə hər vertex`dən başladığı mənbəyə (source) doğru ancaq bir yol var (path), bir vertex`dən mənbəyə doğru 2-ci fərqli bir yol ola bilməz. Və yaxud da bu yol vertex`dən mənbəyə doğru gedib çıxmaya da bilər, ortada rekursiyaya düşmə ehtimalı da var. Bundan sonra bir az sakitləşdim və əl çəkdim) Amma istənilən halda yenə də bacardığım formada kodu implement elədim.
Princeton nümunəsindən fərqli olaraq mən Bellman-Ford alqoritminin “Introduction to Algorithms” (MIT Press) kitabındakı klassik kodlama formasına bənzər bir forma tətbiq elədim:
Məlumat böyük olmadığına görə relax`da performansla bağlı əlavə bir şey tətbiq etmədim, çalışdım daha sadə və başa düşülən olsun. “Negative cycle”ları tapmaq üçün isə indiyə qədər oxuduqlarımı, təsəvvürlərimi cəmləyib məntiqi bir ardıcıllıq qurub öz improvizasiyama uyğun bir metod yazdım. Amma bir “intahası” çıxdı. Düzdür, alqoritm birdən çox arbitrajı imkanını göstərir, amma eyni zamanda arbitraj imkanı olmayan çevrilmələri də göstərir. Alqoritmin fəlsəfəsi belədir ki, (vertex-1) sayda “relax”dan sonra hələ də hansısa vertex üçün daha qısa yol (yaxud daha kiçik dəyər) tapılarsa, deməli həmin vertex “negative cycle”a düşür. Və həmin vertex`dən də başlanğıc (source) vertex`ə doğru geri hərəkət edilərək “path” (yəni valyutalar) tapılır. “Path” dəyərlərini saxlamaq üçün də “predecessor array” istifadə etmişəm, ilk baxışdan başa düşmək sizə bir az çətin gələ bilər, amma diqqətlə nəzər saldıqda məntiqini tutmaq olur. Yəni bu şərtlər pozulmur, amma buna baxmayaraq hərdən elə olur ki, 0.01, 0.001 fərqlə bərabərsizlik ödənilir və vertex “negative cycle”a düşür, lakin arbitraj imkanı olmur. Ola bilər ki, loqarifmə çevirəndə, ya hesablamada haradasa çox cüzi fərq yaranır və bu da sonda belə nəticəyə səbəb olur. Bunun qarşısını almaq üçün kodda dəyişiklik edib ancaq arbitraj imkanı olan nəticələri göstərmək olardı, amma bunu etmədim. Çünki səbəb mənim özümə də maraqlıdır. Bununla bağlı kiminsə hər hansı bir fikri, ideyası olarsa, zəhmət olmasa qeyd etsin.
Yuxarıda qeyd etmişdim ki, data struktur olaraq “adjacency matrix” istifadə etmişəm. Səbəb isə odur ki, bizim nümunədə istifadə edilən valyutaların hər birinin 90-95 % hallarda digərlərinə çevrilməsi mövcuddur. Az-az hallarda ola bilər ki, bazadan əldə edilən məlumatlarda hansısa bir gün üçün TRY və yaxud RUB ilə bağlı məlumatlar heç bir bankda mövcud olmasın. Amma əksər hallarda mövcuddur. Ona görə də spesifik olaraq bu problem üçün “adjacency matrix” data strukturu uyğundur.
Analiz üçün istifadə olunan məlumat tipləri/formaları
Proyektdə az.mm.arbitrage.data paketinə baxsanız 4 class görəcəksiniz:
- AniMezenneData
- AznTodayData
- ExcelData
- JsonData
1. AniMezenneData – yerli bankların 2016.10.29 – 2017.09.17 aralığına aid günlük valyuta məzənnəsi ilə bağlı məlumatlarını əhatə edir. İstifadə olunan məlumatlar http://animezenne.az/ saytına məxsusdur. Alqoritmin analiz edilməsində bu məlumatların çox böyük köməyi oldu, buna görə xüsusi təşəkkürlərimi bildirirəm 🙂 Bu informasiyalar məlumat bazasında saxlanılır və kodda JDBC ilə qoşulub məlumatın əldə edilmə nümunəsini görəcəksiniz. Lokal kompyuterinizdə bunu test edə bilməniz üçün avtomatik baza yaratma scripti işə düşəcək və test üçün sadəcə 2017-ci ilin avqust ayı üzrə məlumatlar əlavə ediləcək. Məlumat bazası kimi MySQL istifadə edilib və təbii ki, bunun üçün kompyuterinizdə MySQL qurulu olmalıdır.
2. AznTodayData – yerli bankların http://azn.today/ saytında verilmiş günlük məzənnə üzrə məlumatlarından istifadə edilir. Məlumatın əldə edilməsi üçün “jsoup” kitabxanasından istifadə edilir və məlumatlar veb səhifənin “page source”dan əldə edilən html-in “parse” edilməsi ilə əldə edilir. Bu kitabxanadan hələ də istifadə etməyənlər üçün maraqlı ola bilər. Sadəcə kod nümunəsində, jsoup ilə əldə edilmiş məlumatların modelə düzgün ardıcıllıqla yerləşdirilməsinə diqqət edin, hərdən indekslərin yeri dəyişir və sonda səhv nəticə verir)
3. ExcelData – yerli bankların excel faylına yazılmış bir günlük məzənnə üzrə məlumatlarını əks etdirir. Proyektdə Apache POI kitabxanası istifadə edilərək excel faylından məlumatın oxunması nümunəsini görəcəksiniz. Excel faylı proyektin daxilində yerləşdirilmişdir, yükləməyə ehtiyac yoxdur. Əgər istəsəniz faylı yükləyib, daxilindəki məlumatları dəyişib yenidən test edə bilərsiniz.
4. JsonData – json hal-hazırda ən işlək məlumat formatlarından biridir, faydalı ola biləcəyini nəzərə alıb bunu da daxil etdim. Kodda API`dən json formatında olan məlumatın əldə edilməsini, necə “parse” edilməsini, Java obyektinə çevrilməsini və istifadə edilməsini görəcəksiniz. Bizdə yerli bankların günlük məzənnə üzrə məlumatlarını verən public API olmadığından test üçün http://fixer.io/ saytına məxsus API`dən istifadə edilib.
Məzənnələrin “cross” edilərək hesablanması
Proyektdə ən önəmli və maraqlı məsələlərdən biri də ən yaxşı valyuta qarşılığının hansı bankda olmasının tapılması, hesablanması idi. Maraqlı nüans olduğu üçün bunu da ayrıca yazmağı qərara aldım.
Bildiyiniz kimi bizdə banklar ancaq manatın xarici valyutalar qarşısında alış və satış qiyməti ilə bağlı məlumatları göstərir, misal üçün heç bir bank USD-EUR qarşılığı ilə bağlı məlumatları göstərmir. Amma alqoritmin işləməsi üçün istifadə edilən bütün valyutaların bir-biri ilə qarşılığını tapmaq lazım idi. Bunun üçün “cross” məzənnə hesablamasını tətbiq etdim. Yəni, USD-EUR qarşılığını tapmaq üçün birinci xarici valyuta (USD) əvvəlcə manata çevrilir və sonra çevrilmiş manat təkrar ikinci xarici valyutaya (EUR) çevrilir. Baxın burada əslində sadə görsənən, amma çox çaşdırıcı olan bir sual çıxır ortaya: manata çevirilərkən alış qiymətimi götürülməlidir yoxsa satış?
AZN – USD–> bu variantda USD-nin ən ucuz satışını təklif edən bank götürülür;USD – AZN–> bu variantda USD-nin ən baha alışını təklif edən bank götürülür;USD – EUR–> bu variantda USD-nin ən baha alışını və EUR-un ən ucuz satışını təklif edən bank götürülməlidir. Amma ən baha alış ilə ən ucuz satış fərqli banklarda ola bilər, bizə isə bir bank üzrə ən yaxşı göstəricini tapmaq lazımdır. “Greedy” yanaşmasını tətbiq edərək iki variantdan birini – USD-nin ən baha alışını və ya EUR-un ən ucuz satışını təklif edən bankı götürə bilərik, amma bu bizə ən yaxşı nəticəni verməyəcək. Ən yaxşı nəticə USD-nin alışının EUR-un satışına nisbətinin ən yüksək olduğu bankdır.
Bunu kodlaşdırmaq da biraz çətinlik yaratdı. Çünki iqtisadi cəhətdən hesablamanı başa düşmək və nəticənin düzgünlüyünü təhlil etmək üçün əsəbləşib kodu əvvəlcə switch ifadədə hər valyuta qarşılığı üçün ayrı-ayrı case`lər şəklində yazmışdım, təxminən 500 sətrə yaxın kod 😀 Amma hər şeyi dəqiqləşdirdikdən sonra kodu dəyişmək lazım idi, çünki həm performans baxımından bərbad idi, həm də səliqəli deyildi, xeyli təkrarçılıq var idi. Sonda beynimi bir az yandırıb kodu zövq ala biləcəyim bir formaya sala bildim. Amma köhnə kodu silməmişəm, kommentə atmışam, kim istəsə daha rahat başa düşmək üçün baxa bilər. Əvvəlcə bankların siyahısına, alış-satış qiymətlərinə baxaq, sonra isə optimal məzənnələrin tapılması koduna baxarıq:
Java kod:
public OptimalRate [][] getOptimalRatesAdjencyMatrix(Data data, String[] cur) {
// cur = {"AZN", "USD", "EUR", "GBP", "RUB", "TRY"};
List<Bank> bankList = data.getBankList();
double currentRate, newRate, r1 = 0, r2 = 0;
OptimalRate R[][] = new OptimalRate[cur.length][cur.length];
for (Bank b : bankList)
for (int i = 0; i < R.length; i++)
for (int j = 0; j < R.length; j++) {
if (i == j){
R[i][j] = new OptimalRate("", 1.);
continue;
}
switch (cur[i]) {
case "AZN": r1 = 1; break;
case "USD": r1 = b.getbUSD(); break;
case "EUR": r1 = b.getbEUR(); break;
case "RUB": r1 = b.getbRUB(); break;
case "GBP": r1 = b.getbGBP(); break;
case "TRY": r1 = b.getbTRY(); break;
}
switch (cur[j]) {
case "AZN": r2 = 1; break;
case "USD": r2 = b.getsUSD(); break;
case "EUR": r2 = b.getsEUR(); break;
case "RUB": r2 = b.getsRUB(); break;
case "GBP": r2 = b.getsGBP(); break;
case "TRY": r2 = b.getsTRY(); break;
}
currentRate = R[i][j] != null ? R[i][j].getValue() : Double.MIN_VALUE;
newRate = r1/r2;
if (r1 > 0 && r2 > 0 && currentRate < newRate)
R[i][j] = new OptimalRate(b.getName(), newRate);
}
return R.clone();
}
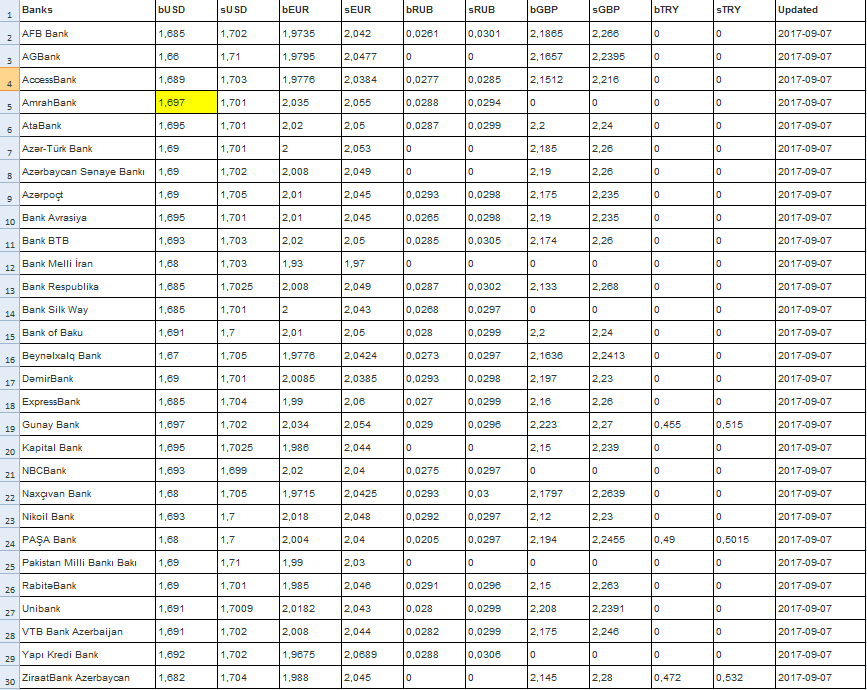
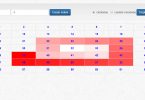
Alınan nəticə isə belədir:
Ümid edirəm bu qədər kifayət edər. Əlavə olaraq qeyd edim ki, bu hesablamaların hər birini ayrı-ayrılıqda yoxlayıb test etmişdim. Amma proyekti “design pattern”ə otuzduranda demək olar ki, hər şeyi “dağıdıb yenidən qurdum”, təkrarçılıqları aradan qaldırmaq üçün mümkün olan çox şeyi ümumiləşdirmişəm. Bu səbəbdən əgər hər hansı bir xəta ilə üzləşsəniz, zəhmət olmasa bildirin.
Bu məsələdən ( və digər səbəblərdən) sonra çox güman ki, alqoritmə bir müddət fasilə verəcəm, bu problem mənə artıqlaması ilə bəs elədi 😀 Amma təcrübədən başa düşdüm ki, alqoritm kodlamaq proyekt kodlamaqdan çox-çox çətindir. Əsas 2 cür çətinlik hiss etdim:
- Sənin problemin üçün lazım olan alqoritmin hansı olduğunu təyin edə bilmək. Çünki yuxarıda da gördünüz ki, Bellman-Ford alqoritmini arbitraj probleminə tətbiq etmək üçün “nə hoqqalardan çıxdıq”)) Bunun ideyasını fikirləşmək belə özlüyündə böyük bir işdir.
- Oxuyub fəlsəfəsini, məntiqini başa düşdüyünüz bir alqoritmi öz real probleminizdə tətbiq etmək. Ola bilər ki, hansısa bir alqoritmi oxuyursunuz, verilən nümunəyə baxırsınız, sadə və rahat gəlir. Amma həmin alqoritmi öz real probleminizə tətbiq edəndə işlər dəyişir. Probleminizin hansısa özəl xüsusiyyətlərindən dolayı xırda dəyişiklik və ya əlavələr etməli olursunuz. Amma misal üçün indeksin
1-dən başlaması əvəzinə sıfırdan başlamasını qeyd edirsinizsə və yaxud>işarəsi əvəzinə>=istifadə edirsinizsə, alqoritmin bütün işləmə fəlsəfəsi alt-üst olur və tamamilə səhv nəticələrə səbəb olur.
Qeyd. Alqoritmi tətbiq edərək real gəlir qazanmaq yerli bazarda müəyyən səbəblərdən dolayı effektiv deyil, sadəcə alqoritmin texniki cəhətdən işlədiyini göstərmək üçün daha tutarlı və maraqlı nümunə olduğu üçün yerli banklar götürülüb. Yenə də istənilən halda iqtisadi və hüquqi məsələlərə görə müəllif məsuliyyət daşımır.
Maven üçün jar`lar:
<dependencies>
<dependency>
<groupId>com.googlecode.princeton-java-introduction</groupId>
<artifactId>introcs</artifactId>
<version>1.0.0</version>
</dependency>
<dependency>
<groupId>org.jsoup</groupId>
<artifactId>jsoup</artifactId>
<version>1.10.3</version>
</dependency>
<dependency>
<groupId>com.ibatis</groupId>
<artifactId>ibatis2-common</artifactId>
<version>2.1.7.597</version>
</dependency>
<dependency>
<groupId>org.apache.poi</groupId>
<artifactId>poi</artifactId>
<version>3.9</version>
</dependency>
<dependency>
<groupId>org.apache.poi</groupId>
<artifactId>poi-ooxml</artifactId>
<version>3.9</version>
</dependency>
<dependency>
<groupId>mysql</groupId>
<artifactId>mysql-connector-java</artifactId>
<version>5.1.24</version>
</dependency>
<dependency>
<groupId>com.googlecode.json-simple</groupId>
<artifactId>json-simple</artifactId>
<version>1.1.1</version>
</dependency>
</dependencies>
1 “Introduction to Algorithms” (MIT Press), 3-cü nəşr, səhifə 679
2 “Algorithms (4th Edition)”, Robert Sedgewick & Kevin Wayne, səhifə 679
3 https://mitpress.mit.edu/sites/default/files/titles/content/Intro_to_Algo_Selected_Solutions.pdf
